题目内容
【题目】如图，在平面直角坐标系中，顶点为（
，
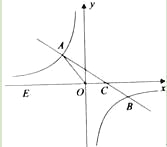
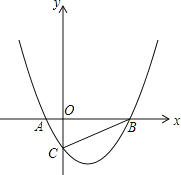
）的抛物线交y轴于点C（0，﹣2），交x轴于点A，B（点A在点B的左侧）．P点是y轴上一动点，Q点是抛物线上一动点．
（1）求抛物线的解析式；
（2）P点运动到何位置时，△POA与△ABC相似？并求出此时P点的坐标；
（3）当以A、B、P、Q四点为顶点的四边形为平行四边形时，求Q点的坐标．
【答案】（1）抛物线为
；（2）P点的坐标为（0，±2），（0，±
）；（3）（﹣5，18），（5，3），（3，﹣2）．
【解析】
（1）设顶点式抛物线解析式，将点C的坐标代入即可；
（2）先求出点A、B的坐标，证明△ACB是直角三角形，分两种对应关系利用三角形相似求出点P的坐标；
（3）分三种情况：①Q点的横坐标为﹣5；②Q点的横坐标为5；③Q点的横坐标为﹣1+4＝3；代入抛物线的解析式求出它们的纵坐标，从而求得Q点的坐标．
解：（1）设抛物线为y＝a（x﹣
）2﹣
，
∵抛物线经过点C（0，﹣2），
∴﹣2＝a（0﹣）2﹣，
a＝．
∴抛物线为；
（2）在原解析式中，令y＝0，则x2﹣x﹣2＝0，
解得x1＝﹣1，x2＝4，
则点A为（﹣1，0），点B为（4，0），
则AB＝5，AC＝
，BC＝2，
∵（）2+（2）2＝52，
∴△ACB是直角三角形，
①设OP的长为x，则有
，
解得x＝2；
②设OP的长为y，则有
，
解得y＝；
则P点的坐标为（0，±2），（0，±）；
（3）因为以A、B、P、Q四点为顶点的四边形为平行四边形，
所以分三种情况：
①Q点的横坐标为﹣5，y＝×（﹣5）2﹣×（﹣5）﹣2＝18；
②Q点的横坐标为5，y＝×52﹣×5﹣2＝3；
③Q点的横坐标为﹣1+4＝3，y＝×32﹣×3﹣2＝﹣2．
所以Q点的坐标为（﹣5，18），（5，3），（3，﹣2）．
练习册系列答案
相关题目
