Question

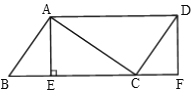
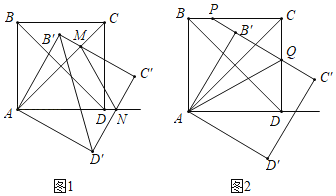
【题目】如图将正方形ABCD绕点A顺时针旋转角度α（0°＜α＜90°）得到正方形AB′C′D′．

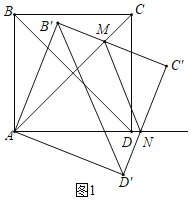
（1）如图1，B′C′与AC交于点M，C′D′与AD所在直线交于点N，若MN∥B′D′，求α；

（2）如图2，C′B′与CD交于点Q，延长C′B′与BC交于点P，当α＝30°时．

①求∠DAQ的度数；

②若AB＝6，求PQ的长度．

Answer 1

【答案】（1）α＝22.5°；（2）①30°；②12﹣4．

【解析】

（1）先根据正方形的性质、旋转的性质、平行线的性质得出，再根据等腰三角形的性质、线段的和差可得，然后根据三角形全等的判定定理与性质可得，最后根据正方形的性质、角的和差即可得；

（2）①先根据旋转的性质可得，再根据正方形的性质、三角形全等的判定定理与性质可得，然后根据角的和差即可得；

②如图2（见解析），设，先根据三角形全等的判定定理与性质得出，再根据直角三角形的性质、平角的定义得出，又根据等腰三角形的性质、三角形的外角性质得出，从而可得，，然后根据线段的和差可求出a的值，从而可得PC的长，最后在中，利用的余弦值即可得．

（1）如图1，由旋转的性质得：

四边形是正方形

四边形是正方形

，，

∴，

∴

∴

∵，

∴，即

∵，

∴

∴

∵

∴

∴

即；

（2）①如图2，由旋转的性质和题意得：

∵

∴

∴

∵

∴

∴；

②如图2，连接AP，在AB上取一点E，使得，连接EP

设

∵，，

∴

∴

∵

∴

∴

∴，

∵

∴

∴，即

∴

在中，，即

解得．