题目内容
【题目】如图,直线l和双曲线y=![]() (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
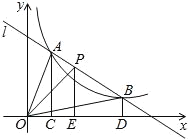
A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3
【答案】D
【解析】
根据双曲线的解析式可得![]() 所以在双曲线上的点和原点形成的三角形面积相等,因此可得S1=S2,设OP与双曲线的交点为P1,过P1作x轴的垂线,垂足为M,则可得△OP1M的面积等于S1和S2 ,因此可比较的他们的面积大小.
所以在双曲线上的点和原点形成的三角形面积相等,因此可得S1=S2,设OP与双曲线的交点为P1,过P1作x轴的垂线,垂足为M,则可得△OP1M的面积等于S1和S2 ,因此可比较的他们的面积大小.
根据双曲线的解析式可得![]()
所以可得S1=S2=![]()
设OP与双曲线的交点为P1,过P1作x轴的垂线,垂足为M
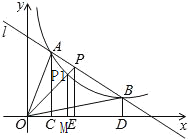
因此![]()
而图象可得![]()
所以S1=S2<S3
故选D

练习册系列答案
相关题目