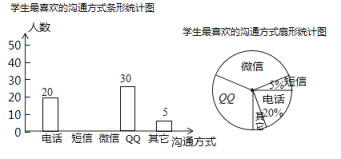
题目内容
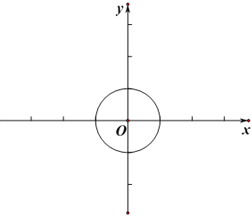
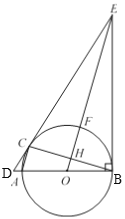
【题目】如图,AB是⊙O的直径,C 是⊙O上一点,过点C 作⊙O的切线,交BA的延长线交于点D,过点B 作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若BF=5,sin∠FBC=![]() ,求AC的长.
,求AC的长.
【答案】(1)见详解;(2)![]()
【解析】
(1)先证EB为⊙O的切线,再利用切线长定理即可证得∠ECB=∠EBC;
(2)先由BF=5,sin∠FBC=![]() 求得FH及HB的长,再由Rt△BOH的勾股定理求得OH长,最后利用中位线即可求得AC的长.
求得FH及HB的长,再由Rt△BOH的勾股定理求得OH长,最后利用中位线即可求得AC的长.
(1)证明:∵BE⊥BA,AB是⊙O的直径,
∴BE是⊙O的切线,
又∵CE是⊙O的切线,
∴BE=CE,
∴∠ECB=∠EBC;
(2)解:如图,连接OC,
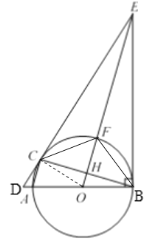
∵BE=CE,OB=OC,
∴OE垂直平分BC,
∴∠BHF=∠BHO=90°,点H为BC的中点,
∴在Rt△BHF中,sin∠FBC=![]() =
=![]() ,
,
∵BF=5,
∴FH=3,
∴BH=![]() ,
,
设OH=x,则OB=OF=x+3,
在Rt△OHB中,OH2+BH2=OB2,
∴x2+42=(x+3)2,
解得x=![]()
∴OH=![]()
∵点O、H分别为AB、CB的中点,
∴OH是△ABC的中位线,
∴AC=2OH=![]()

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目