题目内容
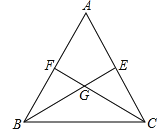
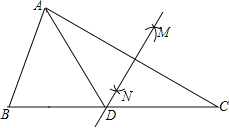
【题目】如图，在△ABC中，按以下步骤作图：①分别以点A和点C为圆心，以大于
AC的长为半径作弧，两弧相交于M、N两点；②作直线MN交BC于点D，连接AD．若AB=BD，AB=6，∠C=30°，则△ACD的面积为_____．
【答案】9
【解析】
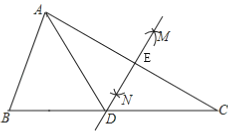
设AC与MN的交点为E，只要证明△ABD是等边三角形，推出BD=AD=DC=AB=6，从而求得DE、CE长，继而求得AC长，再根据三角形面积公式即可求得S△ADC.
如图，由作图可知，MN垂直平分线段AC，设AC与MN的交点为E，
∴DA=DC，
∴∠DAC=∠C=30°，
∴∠ADB=∠C+∠DAC=60°，
∵AB=BD，
∴△ABD是等边三角形，
∴BD=AD=DC=AB=6，
∴DE=3，CE=
，
∴AC=2CE=6，
∴S△ADC=
ACDE=9，
故答案为：9．
练习册系列答案
阅读快车系列答案
相关题目
