题目内容
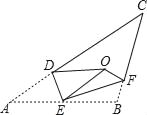
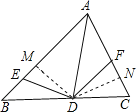
【题目】在△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠EDF+∠EAF=180°,求证DE=DF.

【答案】证明见解析.
【解析】
过D作DM⊥AB,于M,DN⊥AC于N,根据角平分线性质求出DN=DM,继而可推导得出∠MED=∠NFD,根据全等三角形的判定AAS推出△EMD≌△FND即可.
过D作DM⊥AB于M,DN⊥AC于N,
即∠EMD=∠FND=90°,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN(角平分线性质),
∵∠EAF+∠EDF=180°,
∴∠MED+∠AFD=360°-180°=180°,
∵∠AFD+∠NFD=180°,
∴∠MED=∠NFD,
在△EMD和△FND中
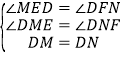 ,
,
∴△EMD≌△FND(AAS),
∴DE=DF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目