题目内容
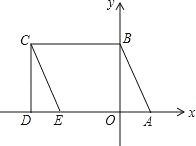
【题目】在直角梯形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,且M在AD上以1cm/s的速度由A向D运动,点N在BC上以2cm/s的速度由C向B运动.
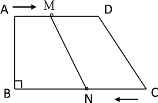
(1)几秒后MNCD为平行四边形?
(2)几秒后ABNM为矩形?
【答案】(1)6秒后,四边形MNCD为平行四边形;(2)7秒后,四边形ABNM为矩形.
【解析】
(1)根据题意可得MA=t,CN=2t,则MD=ADMA=18t,当MD=CN时,四边形MNCD为平行四边形,可得方程18t=2t,解此方程即可求得答案;
(2)由题意可得当MA=BN时,四边形ABNM是矩形,即t=212t时,解此方程即可求得答案.
解:(1)根据题意得:MA=t,CN=2t,则MD=ADMA=18t,
∵AD∥BC,
∴MD∥CN,
∴当MD=CN时,四边形MNCD为平行四边形,
即18t=2t,
解得:t=6,
即6秒后,四边形MNCD为平行四边形;
(2)根据题意得:MA=t,BN=21-2t,
∵AM∥BN,∠B=90°,
∴当MA=BN时,四边形ABNM是矩形,
即t=212t,
解得:t=7,
即7秒后,四边形ABNM为矩形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
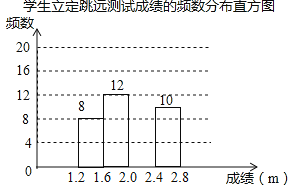
小学生10分钟应用题系列答案【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
【题目】“十一”期间沈阳世博园(10月1日)的进园人数为![]() 万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 |
|
|
|
|
|
|
(1)10月2日的进园人数是多少?
(2)10月1日-10月7日这7天内的进园人数最多的是哪天?最少的是哪天?它们相差多少?