题目内容
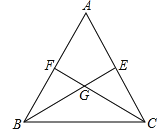
【题目】如图,△ABC的∠ABC和∠ACB的平分线BE,CF相交于点G.求证:
⑴∠BGC=180°-![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
⑵∠BGC=90°+![]() ∠A
∠A
【答案】证明见解析
【解析】
(1)根据角平分线的定义可得∠GBC= ![]() ∠ABC,∠GCB=
∠ABC,∠GCB= ![]() ∠ACB,然后利用三角形的内角和定理列式整理即可;
∠ACB,然后利用三角形的内角和定理列式整理即可;
(2)根据三角形的内角和定理可得∠ABC+∠ACB=180°-∠A,然后代入整理即可得证.
(1)∵∠ABC和∠ACB的平分线BE,CF相交于点G,
∴∠GBC= ![]() ∠ABC,∠GCB=
∠ABC,∠GCB= ![]() ∠ACB,
∠ACB,
∴∠GBC+∠GCB= ![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
在△BCG中,∠BGC=180°-(∠GBC+∠GCB)=180°-![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
即:∠BGC=180°- ![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(2)在△ABC中,∠ABC+∠ACB=180°-∠A,
所以,∠BGC=180°- ![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- ![]() (180°-∠A)=90°+
(180°-∠A)=90°+ ![]() ∠A,
∠A,
即:∠BGC=90°+ ![]() ∠A.
∠A.

【题目】“十一”期间沈阳世博园(10月1日)的进园人数为![]() 万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 |
|
|
|
|
|
|
(1)10月2日的进园人数是多少?
(2)10月1日-10月7日这7天内的进园人数最多的是哪天?最少的是哪天?它们相差多少?
【题目】某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲乙两组学生成绩如下,甲组:30,60,60,60,60,60,70,90,90,100 ;乙组:50,60,60,60,70,70,70,70,80,90.
(1)以上成绩统计分析表中a=______分,b=______分,c=_______分;
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 30% | |
乙组 | b | c | 90% |
(2)小亮同学说:这次竞赛我得了70分,在我们小组中属于中游略偏上,观察上面表格判断,小亮可能是甲乙哪个组的学生?并说明理由
(3)计算乙组的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?并说明理由