Question

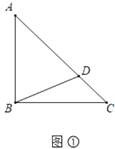
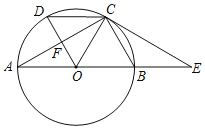
【题目】如图，AB是⊙O的直径，点C是圆周上一点，连接AC、BC，以点C为端点作射线CD、CP分别交线段AB所在直线于点D、P，使∠1＝∠2＝∠A．

（1）求证：直线PC是⊙O的切线；

（2）若CD＝4，BD＝2，求线段BP的长．

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）连接OC，由AB是⊙O的直径证得∠ACO+∠BCO＝90°，由OA=OC证得∠2＝∠A=∠ACO，由此得到∠PCO＝90°，即证得直线PC是⊙O的切线；

（2）利用∠1＝∠A证得∠CDB＝90°，得到CD2＝ADBD，求出AD,由此求得AB=10，OB=5;在由∠OCP＝90°推出OC2＝ODOP，求出OP＝，由此求得线段BP的长.

（1）连接OC，

∵AB是⊙O的直径，

∴∠ACB＝90°，

∴∠ACO+∠BCO＝90°，

∵OA＝OC，

∴∠A＝∠ACO，

∵∠A＝∠1＝∠2，

∴∠2＝∠ACO，

∴∠2+∠BCO＝90°，

∴∠PCO＝90°，

∴OC⊥PC，

∴直线PC是⊙O的切线；

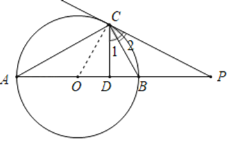
（2）∵∠ACB＝90°，

∴∠A+∠ABC＝90°

∴∠1＝∠A，

∴∠1+∠ABC＝90°，

∴∠CDB＝90°，

∴CD2＝ADBD，

∵CD＝4，BD＝2，

∴AD＝8，

∴AB＝10，

∴OC＝OB＝5，

∵∠OCP＝90°，CD⊥OP，

∴OC2＝ODOP，

∴52＝（5﹣2）×OP，

∴OP＝，

∴PB＝OP﹣OB＝．