题目内容
【题目】(问题提出)
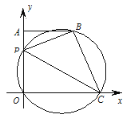
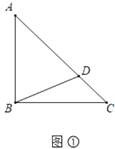
(1)如图①,在等腰![]() 中,斜边
中,斜边![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,则
,则![]() 的最小值为 .
的最小值为 .
(问题探究)
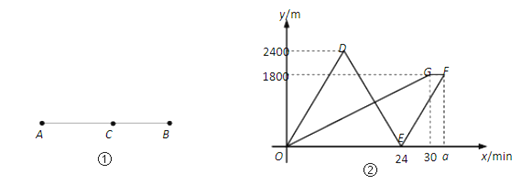
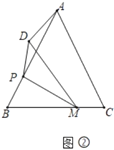
(2)如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,点
,点![]() 与点
与点![]() 对应,连接
对应,连接![]() ,求
,求![]() 的最小值.
的最小值.
(问题解决)
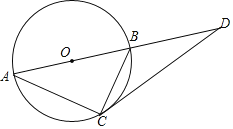
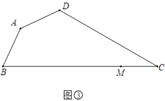
(3)如图③,四边形![]() 是规划中的休闲广场示意图,其中
是规划中的休闲广场示意图,其中![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() .现计划在四边形
.现计划在四边形![]() 内选取一点
内选取一点![]() ,把
,把![]() 建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路
建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路![]() 、
、![]() ,从实用和美观的角度,要求满足
,从实用和美观的角度,要求满足![]() ,且景观绿化区面积足够大,即
,且景观绿化区面积足够大,即![]() 区域面积尽可能小.则在四边形
区域面积尽可能小.则在四边形![]() 内是否存在这样的点
内是否存在这样的点![]() ?若存在,请求出
?若存在,请求出![]() 面积的最小值;若不存在,请说明理由.
面积的最小值;若不存在,请说明理由.
【答案】(1)2;(2)![]() ;(3)存在点
;(3)存在点![]() ,使得
,使得![]() 的面积最小,
的面积最小,![]() 面积的最小值是
面积的最小值是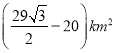 .
.
【解析】
(1)BD的最小值即BD⊥AC的情况;
(2)以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,此时
,此时![]() 值(即A
值(即A![]() )最小;
)最小;
(3)作![]() 的外接圆
的外接圆![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于点
于点![]() 即为所求位置
即为所求位置
(1)当![]() 时,如图1,
时,如图1,
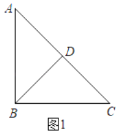
∵![]() ,∴
,∴![]() 是
是![]() 的中点,
的中点,
∴![]() ,即
,即![]() 的最小值是2.
的最小值是2.
故答案为:2;
(2)如图2,由题意得:![]() ,
,
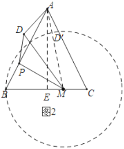
∴点![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的
为半径的![]() 上,连接
上,连接![]() 交
交![]() 于点
于点![]() ,此时
,此时![]() 值最小,
值最小,
过![]() 作
作![]() 于
于![]() ,
,
∵![]() ,∴
,∴![]() ,
,
由勾股定理得:![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
即线段![]() 长的最小值是
长的最小值是![]() ;
;
(3)如图3,假设在四边形![]() 中存在点
中存在点![]() ,
,
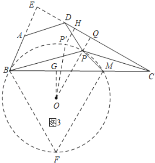
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
以![]() 为边向下作等边
为边向下作等边![]() ,作
,作![]() 的外接圆
的外接圆![]() ,
,
∵![]() ,则点
,则点![]() 在
在![]() 上,
上,
过![]() 作
作![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,
,
设点![]() 是
是![]() 上任意一点,连接
上任意一点,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
可得![]() ,即
,即![]() ,
,
∴![]() 即为所求的位置,
即为所求的位置,
延长![]() ,
,![]() 交于点
交于点![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
过![]() 作
作![]() 于
于![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴存在点![]() ,使得
,使得![]() 的面积最小,
的面积最小,![]() 面积的最小值是
面积的最小值是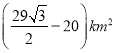 .
.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案【题目】为了增强学生对新冠病毒预防知识的了解,我校初一年级开展了网上预防知识的宣传教育活动.为了解这次宣传教育活动的效果,学校从初一年级1500名学生中随机抽取部分学生进行网上知识测试(测试满分100分,得分均为整数),并根据抽取的学生测试成绩,制作了如下统计图表:
抽取学生知识测试成绩的频数表 | ||
成绩 | 频数(人) | 频率 |
| 10 | 0.1 |
| 15 |
|
|
| 0.2 |
| 40 |
|
|
|
|
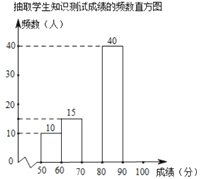
由图表中给出的信息回答下列问题:
(1)![]() ,
,![]() ,并补全频数直方图;
,并补全频数直方图;
(2)如果80分以上(包括80分)为优秀,请估计初一年级1500名学生中成绩优秀的人数;
(3)小强在这次测试中成绩为85分,你认为85分一定是这100名学生知识测试成绩的中位数吗?请简要说明理由.