题目内容
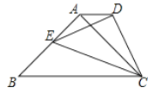
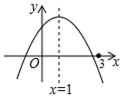
【题目】已知直线y1＝﹣x+2和抛物线
相交于点A，B．
(1)当k＝
时，求两函数图象的交点坐标；
(2)二次函数y2的顶点为P，PA或PB与直线y1＝﹣x+2垂直时，求k的值．
(3)当﹣4＜x＜2时，y1＞y2，试直接写出k的取值范围．
【答案】(1)A(2，0)，B(﹣
，
)；(2)1或-
；(3) 
＜k＜
且k≠0.
【解析】
（1）联立方程组
即可求交点；
（2）当PA与y1=-x+2垂直时，k=1；当PB与y1=-x+2垂直时，k=-；
（3）当x=-4时，y1＞y2，6＞24k；只有开口向上时成立，所以k＞0；
(1)当k＝
时，
，
联立方程组，
∴
或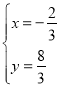
，
∴A(2，0)，B(﹣，)；
(2)
的顶点P(1，﹣k)，
当PA与y1＝﹣x+2垂直时，k＝1；
当PB与y1＝﹣x+2垂直时，k＝﹣；
(3)当x＝2时，y1＝y2＝0，
当x＝﹣4时，y1＞y2，
当k＞0时，
∴6＞24k，
∴k＜，
∴0＜k＜；
当k＜0时，直线与抛物线有一个交点时：-x+2=kx2-2kx，
∵△=（1+2k）2=0，
∴k=，
∴＜k＜0；
综上所述；＜k＜且k≠0；
【题目】为了增强学生对新冠病毒预防知识的了解，我校初一年级开展了网上预防知识的宣传教育活动．为了解这次宣传教育活动的效果，学校从初一年级1500名学生中随机抽取部分学生进行网上知识测试（测试满分100分，得分均为整数），并根据抽取的学生测试成绩，制作了如下统计图表：
抽取学生知识测试成绩的频数表 | ||
成绩 | 频数（人） | 频率 |
| 10 | 0.1 |
| 15 |
|
|
| 0.2 |
| 40 |
|
|
|
|
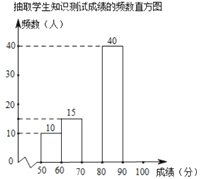
由图表中给出的信息回答下列问题：
（1）
，
，并补全频数直方图；
（2）如果80分以上（包括80分）为优秀，请估计初一年级1500名学生中成绩优秀的人数；
（3）小强在这次测试中成绩为85分，你认为85分一定是这100名学生知识测试成绩的中位数吗？请简要说明理由．
