ЬтФПФкШн
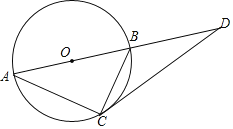
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпAByЃНkxЉ1ЗжБ№НЛxжсЁЂyжсгкЕуAЁЂBЃЌжБЯпCDyЃНx+2ЗжБ№НЛxжсЁЂyжсгкЕуDЁЂCЃЌЧвжБЯпABЁЂCDНЛгкЕуEЃЌEЕФКсзјБъЮЊЉ6ЃЎ
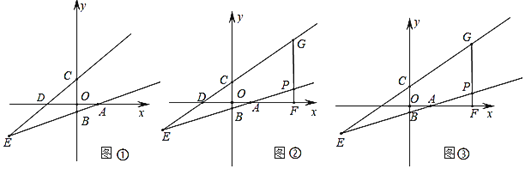
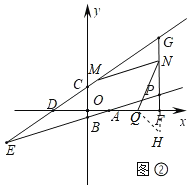
(1)ШчЭМЂйЃЌЧѓжБЯпABЕФНтЮіЪНЃЛ
(2)ШчЭМЂкЃЌЕуPЮЊжБЯпBAЕквЛЯѓЯоЩЯвЛЕуЃЌЙ§PзїyжсЕФЦНааЯпНЛжБЯпCDгкGЃЌНЛxжсгкFЃЌдкЯпЖЮPGШЁЕуNЃЌдкЯпЖЮAFЩЯШЁЕуQЃЌЪЙGNЃНQFЃЌдкDGЩЯШЁЕуMЃЌСЌНгMNЁЂQNЃЌШєЁЯGMNЃНЁЯQNFЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
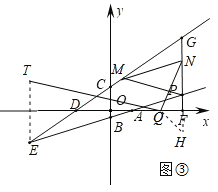
(3)дк(2)ЕФЬѕМўЯТЃЌЕуEЙигкxжсЖдГЦЕуЮЊTЃЌСЌНгMPЁЂTQЃЌШєMPЁЮTQЃЌЧвGNЃКNPЃН4ЃК3ЃЌЧѓЕуPЕФзјБъЃЎ
ЁОД№АИЁП(1)yЃН![]() xЉ1ЃЛ(2)
xЉ1ЃЛ(2)![]() =
=![]() ЃЛ(3)ЕуPзјБъЮЊ(8ЃЌ3).
ЃЛ(3)ЕуPзјБъЮЊ(8ЃЌ3).
ЁОНтЮіЁП
(1)АбЕуEКсзјБъДњШыжБЯпCDЧѓЕУЕуEЕФзјБъЃЌдйДњШыжБЯпyЃНkxЉ1жаЃЌМДЧѓЕУжБЯпABЕФНтЮіЪНЃЎ
(2)ЯШЧѓГіЕуCЁЂDзјБъЕУЕНЕШбќRtЁїOCDЃЌгЩGFЁЮyжсЕУЁїDGFвВЪЧЕШбќжБНЧШ§НЧаЮЃЌвзЕУDGЃН![]() FGЃЎЙЪбгГЄбгГЄGFжСHЃЌЪЙFHЃНFQЙЙдьЕШбќжБНЧШ§НЧаЮЃЎжЄУїЁїGMNЁзЁїHNQЃЌгЩЖдгІЯпЖЮГЩБШР§ЕУNHЃН
FGЃЎЙЪбгГЄбгГЄGFжСHЃЌЪЙFHЃНFQЙЙдьЕШбќжБНЧШ§НЧаЮЃЎжЄУїЁїGMNЁзЁїHNQЃЌгЩЖдгІЯпЖЮГЩБШР§ЕУNHЃН![]() MGЃЎдйЭЈЙ§зЊЛЏжЄУїFGЃНNHЃЌДњШыМЦЫуЕУЕНDGЃН2MGЃЌМДMЮЊDGжаЕуЃЌНјЖјЧѓЕУ
MGЃЎдйЭЈЙ§зЊЛЏжЄУїFGЃНNHЃЌДњШыМЦЫуЕУЕНDGЃН2MGЃЌМДMЮЊDGжаЕуЃЌНјЖјЧѓЕУ![]() =
=![]() ЃЎ
ЃЎ
(3)ЩшЕуPКсзјБъЮЊpЃЌдђФмгУpБэЪОGЁЂFЁЂMЕФзјБъЃЌНјЖјгУpБэЪОGPЕФГЄЃЎгЩGNЃКNPЃН4ЃК3ЃЌЧѓЕУгУpБэЪОGNЕФЪНзгЃЌгжвђЮЊGNЃНQFЃЌМДФмгУpБэЪОQЕФзјБъЃЎвзЧѓЕуTзјБъЃЌЙЪФмгУД§ЖЈЯЕЪ§ЗЈЧѓжБЯпTQНтЮіЪНжавЛДЮЯюЯЕЪ§aЕФЪНзг(КЌp)ЃЎЭЌРэПЩЧѓжБЯпMPНтЮіЪНжавЛДЮЯюЯЕЪ§cЕФЪНзг(КЌp)ЃЌгЩMPЁЮTQПЩЕУaЃНcЃЌМДСаЕУЙигкpЕФЗНГЬЃЌЧѓГіpМДЕУЕуPзјБъЃЎ
НтЃК(1)НЋxЃНЉ6ДњШыyЃНx+2жаЕУyЃНЉ4
ЁрE(Љ6ЃЌЉ4)ЃЌ
НЋE(Љ6ЃЌЉ4)ДњШыyЃНkxЉ1жаЃЌ
ЕУЉ4ЃНЉ6kЉ1ЃЌНтЕУkЃН![]() ЃЌ
ЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊyЃН![]() xЉ1
xЉ1
(2)ШчЭМЂкЃЌбгГЄGFжСHЃЌЪЙFHЃНFQЃЌСЌНгQHЃЌ
ЁпЁЯQFHЃН90ЁуЃЌGNЃНQF
ЁрQHЃН![]() FQЃН
FQЃН![]() GNЃЌЁЯNHQЃН45Ёу
GNЃЌЁЯNHQЃН45Ёу
дкyЃНx+2жаСюxЃН0ЃЌЕУyЃН2ЃЌСюyЃН0ЃЌЕУxЃНЉ2ЃЌ
ЁрC(0ЃЌ2)ЃЌD(Љ2ЃЌ0)ЃЌ
ЁрOCЃНODЃН2
ЁпЁЯCODЃН90Ёу
ЁрЁЯOCDЃНЁЯODCЃН45Ёу
ЁпFGЁЮOC
ЁрЁЯDGFЃНЁЯDCOЃН45ЁуЃЌЁЯDFGЃНЁЯCODЃН90Ёу
ЁрDGЃН![]() FGЃЌЁЯMGNЃНЁЯNHQЃН45Ёу
FGЃЌЁЯMGNЃНЁЯNHQЃН45Ёу
ЁпЁЯGMNЃНЁЯQNF
ЁрЁїGMNЁзЁїHNQ
Ёр![]()
ЁрNHЃН![]() MG
MG
ЁпGNЃНFQЃНFH
ЁрFN+GNЃНFN+FHЃЌМДFGЃНNH
ЁрDGЃН![]() FGЃН
FGЃН![]() NHЃН
NHЃН![]() ЁС
ЁС![]() MGЃН2MG
MGЃН2MG
ЁрDGЃНDM+MGЃН2MG
ЁрDMЃНMGЃН![]() DG
DG
Ёр![]() =
=![]() =
=![]()
(3)ШчЭМЂлЃЌЕуTгыEЙигкxжсЖдГЦЃЌ
ЁрT(Љ6ЃЌ4)
ЁпЕуPдкжБЯпBAЕквЛЯѓЯоЩЯ
ЁрЩшЕуPзјБъЮЊ(pЃЌ![]() pЉ1)(pЃО2)
pЉ1)(pЃО2)
ЁпFGЁЮyжс
ЁрF(pЃЌ0)ЃЌG(pЃЌp+2)ЃЌ
ЁрPFЃН![]() pЉ1ЃЌGFЃНp+2
pЉ1ЃЌGFЃНp+2
ЁрGPЃНGFЉPFЃН![]() p+3
p+3
ЁпGNЃКNPЃН4ЃК3
ЁрFQЃНGNЃН![]() GPЃН
GPЃН![]()
ЁрxQЃНpЉ![]() ЃЌМДQ(
ЃЌМДQ(![]() ЃЌ0)
ЃЌ0)
ЩшжБЯпTQНтЮіЪНЮЊЃКyЃНax+b
Ёр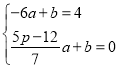 НтЕУЃКaЃН
НтЕУЃКaЃН![]()
Ёп![]() =
=![]() ЃЌМДЕуMЮЊDGжаЕу
ЃЌМДЕуMЮЊDGжаЕу
ЁрM(![]() ЃЌ
ЃЌ![]() )
)
ЩшжБЯпMPНтЮіЪНЮЊЃКyЃНcx+d
Ёр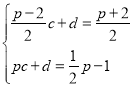 НтЕУЃКcЃН
НтЕУЃКcЃН![]()
ЁпMPЁЮTQ
ЁрaЃНcЃЌМД![]()
НтЕУЃКpЃН8
ЁрЕуPзјБъЮЊ(8ЃЌ3)

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПФГаЃГѕШ§НјааСЫЕкШ§ДЮФЃФтПМЪдЃЌИУаЃСьЕМЮЊСЫСЫНтбЇЩњЕФЪ§бЇПМЪдЧщПіЃЌГщбљЕїВщВПЗжбЇЩњЕФЪ§бЇГЩМЈЃЌВЂНЋГщбљЕФЪ§ОнНјааСЫШчЯТећРэЃК
ЂйШчЯТЗжЪ§ЖЮећРэбљБОЃЛ
ЕШМЖЕШМЖ | ЗжЪ§ЖЮ | ИїзщзмЗж | ШЫЪ§ |
A | 110ЃМXЃМ120 | P | 4 |
B | 100ЃМXЃМ110 | 843 | n |
C | 90ЃМXЁм100 | 574 | m |
D | 80ЃМXЃМ90 | 171 | 2 |
ЂкИљОнзѓБэЛцжЦЩШаЮЭГМЦЭМЃЎ

ЃЈ1ЃЉЬюПеmЃНЁЁ ЁЁЃЌnЃНЁЁ ЁЁЃЌЪ§бЇГЩМЈЕФжаЮЛЪ§ЫљдкЕФЕШМЖЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЙћИУаЃга1200УћбЇЩњВЮМгСЫБОДЮФЃФтВтЃЌЙРМЦDЕШМЖЕФШЫЪ§ЃЛ
ЃЈ3ЃЉвбжЊГщбљЕїВщбЇЩњЕФЪ§бЇГЩМЈЦНОљЗжЮЊ102ЗжЃЌЧѓAЕШМЖбЇЩњЕФЪ§бЇГЩМЈЕФЦНОљЗжЪ§ЃЎ