题目内容
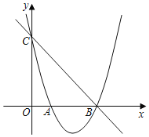
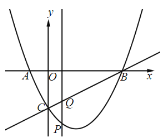
【题目】如图,在平面直角坐标系中,抛物线![]() 过点
过点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴下方的抛物线上一动点(包含点
轴下方的抛物线上一动点(包含点![]() ,
,![]() ).作直线
).作直线![]() ,若过点
,若过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)在点![]() 运动的过程中,请求出
运动的过程中,请求出![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(3)在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,使
,使![]() 是等腰三角形.若存在,请直接写出点
是等腰三角形.若存在,请直接写出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 面积的最大值为5,此时点
面积的最大值为5,此时点![]() 的坐标为
的坐标为![]() ;(3)存在,点
;(3)存在,点![]() 的横坐标为2,1.5或
的横坐标为2,1.5或![]() .
.
【解析】
(1)将A、B两点坐标代入函数解析式计算即可;
(2)先求出直线BC的解析式,设点![]() 的横坐标为
的横坐标为![]() ,当点
,当点![]() 在直线
在直线![]() 下方时,
下方时,![]() ,先求出PQ的最大值,进而得到
,先求出PQ的最大值,进而得到![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标,当点
的坐标,当点![]() 在直线
在直线![]() 上方时,
上方时,![]() ,同样求出PQ的最大值,进而得到
,同样求出PQ的最大值,进而得到![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标,最后两者比较大小即可;
的坐标,最后两者比较大小即可;
(3)分别讨论当CQ=CP,CQ=QP及CP=QP时,画出相应图形,构造直角三角形利用勾股定理计算即可.
解:(1)根据题意,抛物线的解析式可写为:![]() ,
,
即![]() ,
,
![]() ,
,![]() .
.
∴ 该抛物线的解析式为![]() .
.
(2)如图,连接![]() ,
,![]() .
.
将![]() 代入
代入![]() 得,
得,![]() .
.
![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
将![]() ,
,![]() 代入
代入![]() 得,
得,
![]()
解得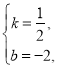
∴直线![]() 的解析式为:
的解析式为:![]() .
.
设点![]() 的横坐标为
的横坐标为![]() ,
,
当点![]() 在直线
在直线![]() 下方时,
下方时,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() 最大,此时,
最大,此时,![]() .
.
∴![]() 面积的最大值为:
面积的最大值为:![]() .
.
当点![]() 在直线
在直线![]() 上方时,
上方时,![]() ,
,
∴![]()
∴当![]() 时,
时,![]() 最大,此时,
最大,此时,![]() .
.
∴![]() 面积的最大值为:
面积的最大值为:![]() .
.
∵![]() ,
,
∴![]() 面积的最大值为5,此时点
面积的最大值为5,此时点![]() 的坐标为
的坐标为![]()
(3)设点![]() 的横坐标为
的横坐标为![]() ,则
,则![]() ,
,![]() ,
,
∴PQ=|![]() |=|
|=|![]() |,
|,
如图,当CQ=CP时,过点C作CH⊥PQ,
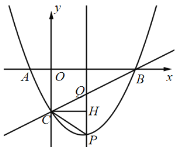
则PQ=2QC,
∵点C(0,-2),
∴QC=|![]() |=|
|=|![]() |,
|,
∴|![]() |=2|
|=2|![]() |,
|,
解得m=2或m=0(舍去)
如图,当CQ=QP时,则CQ=QP=|![]() |,
|,

过点C作CH⊥PQ,则CH=|m|,QH=|![]() |,
|,
在Rt△QCH中,QC2=QH2+CH2,
∴ ,
,
解得m=![]() 或m=
或m=![]() (舍去)或m=0(舍去),
(舍去)或m=0(舍去),
如图,当CP=QP时,则CP=QP=|![]() |,
|,

过点C作CH⊥PQ,则CH=|m|,PH=|![]() |=|
|=|![]() |,
|,
在Rt△PCH中,PC2=PH2+CH2,
∴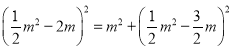 ,
,
解得m=1.5,
∴存在点![]() ,使
,使![]() 是等腰三角形,点
是等腰三角形,点![]() 的横坐标为2,1.5或
的横坐标为2,1.5或![]() .
.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查部分学生的数学成绩,并将抽样的数据进行了如下整理:
①如下分数段整理样本;
等级等级 | 分数段 | 各组总分 | 人数 |
A | 110<X<120 | P | 4 |
B | 100<X<110 | 843 | n |
C | 90<X≤100 | 574 | m |
D | 80<X<90 | 171 | 2 |
②根据左表绘制扇形统计图.

(1)填空m= ,n= ,数学成绩的中位数所在的等级 ;
(2)如果该校有1200名学生参加了本次模拟测,估计D等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A等级学生的数学成绩的平均分数.