Question

【题目】如图，已知为的直径，，点和点是上关于直线对称的两个点，连接、，且，直线和直线相交于点，过点作直线与线段的延长线相交于点，与直线相交于点，且．

（1）求证：直线为的切线；

（2）若点为线段上一点，连接，满足，

①求证：；

②求的最大值．

Answer 1

【答案】（1）见解析；（2）①见解析；②5．

【解析】

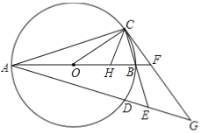
（1）由题意可知：∠CAB＝∠GAF，由圆的性质可知：∠CAB＝∠OCA，所以∠OCA＝∠GCE，从而可证明直线CG是⊙O的切线；

（2）①由于CB＝CH，所以∠CBH＝∠CHB，易证∠CBH＝∠OCB，从而可证明△CBH∽△OBC；

②由△CBH∽△OBC可知：，所以，由于BC＝HC，所以，利用二次函数的性质即可求出OH＋HC的最大值．

（1）由题意可知：，

∵是的直径，

∴

∵

∴，

∴，

∵

∴，

∵是的半径，

∴直线是的切线；

（2）①∵，

∴，

∵，

∴，

∴

②由可知：

∵，

∴，

∴

∴

∵

∴，

当，此时

∵，

∴，

令,

∴

当时，

∴可取得最大值，最大值为5．