题目内容
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.
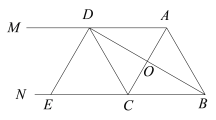
(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)由ASA即可得出结论;
(2)先证明四边形ABCD是平行四边形,再证明AD=AB,即可得出结论;
(3)由菱形的性质得出AC⊥BD,证明四边形ACED是平行四边形,得出AC=DE=2,AD=EC,由菱形的性质得出EC=CB=AB=2,得出EB=4,由勾股定理得BD═![]() ,即可得出答案.
,即可得出答案.
(1)∵点O是AC的中点,
∴AO=CO,
∵AM∥BN,
∴∠DAC=∠ACB,
在△AOD和△COB中,
 ,
,
∴△ADO≌△CBO(ASA);
(2)由(1)得△ADO≌△CBO,
∴AD=CB,
又∵AM∥BN,
∴四边形ABCD是平行四边形,
∵AM∥BN,
∴∠ADB=∠CBD,
∵BD平分∠ABN,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AD=AB,
∴平行四边形ABCD是菱形;
(3)由(2)得四边形ABCD是菱形,
∴AC⊥BD,AD=CB,
又DE⊥BD,
∴AC∥DE,
∵AM∥BN,
∴四边形ACED是平行四边形,
∴AC=DE=2,AD=EC,
∴EC=CB,
∵四边形ABCD是菱形,
∴EC=CB=AB=2,
∴EB=4,
在Rt△DEB中,由勾股定理得BD=![]() =
=![]() ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查部分学生的数学成绩,并将抽样的数据进行了如下整理:
①如下分数段整理样本;
等级等级 | 分数段 | 各组总分 | 人数 |
A | 110<X<120 | P | 4 |
B | 100<X<110 | 843 | n |
C | 90<X≤100 | 574 | m |
D | 80<X<90 | 171 | 2 |
②根据左表绘制扇形统计图.

(1)填空m= ,n= ,数学成绩的中位数所在的等级 ;
(2)如果该校有1200名学生参加了本次模拟测,估计D等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A等级学生的数学成绩的平均分数.
【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.收集数据:随机抽取甲乙两所学校的名学生的数学成绩进行
甲 91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙 84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理、描述数据:按如下数据段整理、描述这两组数据,分析数据:
分段 学校 |
|
|
|
|
|
|
|
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 |
| 91 | 268.43 |
乙 | 81.95 | 86 | 88 | 115.25 |
(1)经统计,表格中![]() 的值是__________.
的值是__________.
(2)得出结论
①若甲学校有600名初二学生,估计这次考试成绩80分以上人数为__________.
②可以推断出__________学校学生的数学水平较高,理由为:__________.(至少从两个不同的角度说明推断的合理性)