Question

【题目】如图，直线y=﹣ 与x轴、y轴分别交于点A、B；点Q是以C（0，﹣1）为圆心、1为半径的圆上一动点，过Q点的切线交线段AB于点P，则线段PQ的最小是 ．

Answer 1

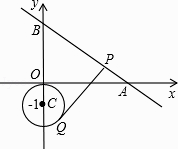
【答案】
【解析】解：过点C作CP⊥直线AB于点P，过点P作⊙C的切线PQ，切点为Q，此时PQ最小，连接CQ，如图所示．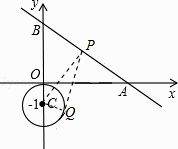

当x=0时，y=3，
∴点B的坐标为（0，3）；
当y=0时，x=4，
∴点A的坐标为（4，0）．
∴OA=4，OB=3，
∴AB= =5，
∴sinB= = ．
∵C（0，﹣1），
∴BC=3﹣（﹣1）=4，
∴CP=BCsinB= ．
∵PQ为⊙C的切线，
∴在Rt△CQP中，CQ=1，∠CQP=90°，
∴PQ= = ．
故答案为： ．
过点C作CP⊥直线AB与点P，过点P作⊙C的切线PQ，切点为Q，此时PQ最小，连接CQ，利用角的正弦求出CP的值，再根据勾股定理即可求出PQ的长度．