题目内容
【题目】如图所示,在△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN,CE⊥MN,垂足分别为D,E.
(1)求证:①∠BAD=∠ACE;②BD=AE.
(2)请写出BD,CE,DE三者间的数量关系式,并证明.

【答案】见解析
【解析】
(1)①由直角三角形两锐角互余可得∠BAD+∠CAE=90°,∠ACE+∠CAE=90°,从而即可证得∠BAD=∠ACE;
②通过证明△ABD≌△CAE,根据全等三角形的对应边相等即可得BD=AE;
(2)BD=CE+DE,由△ABD≌△CAE,利用全等三角形对应边相等可得BD=AE,AD=CE,由AE=AD+DE,即可得到BD=CE+DE.
(1)证明:①∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵CE⊥MN,∴∠ACE+∠CAE=90°,
∴∠BAD=∠ACE;
②∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
在△ABD和△CAE中,
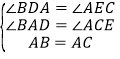 ,
,
∴△ABD≌△CAE,
∴BD=AE;
(2)BD=CE+DE.证明如下:
∵△ABD≌△CAE,
∴BD=AE,AD=CE.
∵AE=AD+DE,
∴BD=CE+DE.

练习册系列答案
相关题目