题目内容
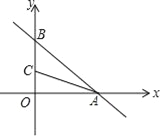
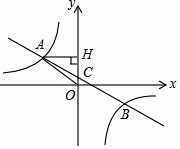
【题目】如图,一次函数y=ax+b的图象与反比例函数y= ![]() 的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=
的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 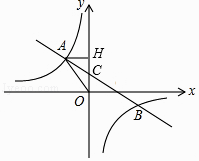
(1)求△AHO的周长;
(2)求反比例函数和一次函数的解析式.
【答案】
(1)解:∵AH⊥y轴于点H,
∴∠AHO=90°,
∴tan∠AOH= ![]() ,AH=4,
,AH=4,
∴OH=3,
∴由勾股定理可求出OA=5,
∴△AHO的周长为3+4+5=12
(2)解:由(1)可知:点A的坐标为(﹣4,3),
把(﹣4,3)代入y= ![]() ,可得k=﹣12,
,可得k=﹣12,
∴反比例函数的解析式为:y=﹣ ![]() ,
,
∵把B(m,﹣2)代入反比例函数y=﹣ ![]() 中,可得m=6,
中,可得m=6,
∴点B的坐标为(6,﹣2),
将A(﹣4,3)和B(6,﹣2)代入y=ax+b,可得
![]() ,
,
解得:  ,
,
∴一次函数的解析式为:y=﹣ ![]() x+1
x+1
【解析】(1)根据tan∠AOH= ![]() 求出AH的长度,由勾股定理可求出OH的长度即可求出△AHO的周长.(2)根据点A的坐标为(﹣4,3),点A在反比例函数的图象上,可求出k的值,将点B的坐标代入反比例函数的解析式中求出m的值,然后将A、B两点的坐标代入一次函数解析式中即可求出该一次函数的解析式.
求出AH的长度,由勾股定理可求出OH的长度即可求出△AHO的周长.(2)根据点A的坐标为(﹣4,3),点A在反比例函数的图象上,可求出k的值,将点B的坐标代入反比例函数的解析式中求出m的值,然后将A、B两点的坐标代入一次函数解析式中即可求出该一次函数的解析式.
【考点精析】根据题目的已知条件,利用确定一次函数的表达式和解直角三角形的相关知识可以得到问题的答案,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目