Question

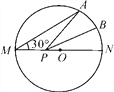
【题目】如图，AB为⊙O的直径，CD为弦，且CD⊥AB，垂足为H．

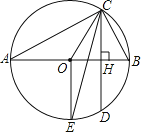
（1）若∠BAC=30°，求证：CD平分OB．

（2）若点E为弧ADB的中点，连接0E，CE．求证：CE平分∠OCD．

（3）若⊙O的半径为4，∠BAC=30°，则圆周上到直线AC距离为3的点有多少个？请说明理由．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）2，理由见解析.

【解析】

试题（1）根据圆周角定理由AB为⊙O的直径得到∠ACB=90°，而∠BAC=30°，所以∠B=60°，于是可判断△OBC为等边三角形，根据等边三角形的性质由CD⊥OB易得CD平分OB；

（2）由点E为的中点，根据垂径定理的推论得OE⊥AB，则OE∥CD，根据平行线的性质得∠OEC=∠ECD，而∠OEC=∠OCE，所以∠OCE=∠ECD；

（3）作OF⊥AC于F，交⊙O于G，根据含30度的直角三角形三边的关系得OF=OA=2，则GF=OG-OF=2，于是可得到在弧AC上没有一个点到AC的距离为3cm，在弧AEC上有两个点到AC的距离为3cm．

试题解析：（1）证明：∵AB为⊙O的直径，

∴∠ACB=90°，

∵∠BAC=30°，

∴∠B=60°，

而OC=OB，

∴△OBC为等边三角形，

∵CD⊥OB，

∴CD平分OB；

（2）证明：∵点E为的中点，

∴OE⊥AB，

而CD⊥AB，

∴OE∥CD

∴∠OEC=∠ECD，

∵OC=OE，

∴∠OEC=∠OCE，

∴∠OCE=∠ECD，

即CE平分∠OCD；

（3）圆周上到直线AC距离为3的点有2个．理由如下：

作OF⊥AC于F，交⊙O于G，如图，

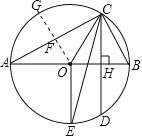
∵OA=4，∠BAC=30°，

∴OF=OA=2，

∴GF=OG-OF=2，即在上到AC的最大距离为2cm，

∴在上没有一个点到AC的距离为3cm，

而在上到AC的最大距离为6cm，

∴在上有两个点到AC的距离为3cm．

考点: 圆的综合题.