题目内容
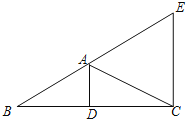
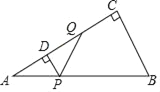
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A、B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当点Q与点C重合时,求t的值;
(3)设△PDQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.
【答案】(1)CD= 2![]() ﹣
﹣![]() t(0<t<2);(2)1;(3)见解析;(4)t的值为
t(0<t<2);(2)1;(3)见解析;(4)t的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)先求出AC,用三角函数求出AD,即可得出结论;
(2)利用AD+DQ=AC,即可得出结论;
(3)分两种情况,利用三角形的面积公式和面积差即可得出结论;
(4)分三种情况,利用锐角三角函数,即可得出结论.
(1)在Rt△ABC中,∠A=30°,AB=4,
∴AC=2![]() ,
,
∵PD⊥AC,
∴∠ADP=∠CDP=90°,
在Rt△ADP中,AP=2t,
∴DP=t,AD=APcosA=2t×![]() =
=![]() t,
t,
∴CD=AC﹣AD=2![]() ﹣
﹣![]() t(0<t<2);
t(0<t<2);
(2)在Rt△PDQ中,∵∠DPC=60°,
∴∠PQD=30°=∠A,
∴PA=PQ,
∵PD⊥AC,
∴AD=DQ,
∵点Q和点C重合,
∴AD+DQ=AC,
∴2×![]() t=2
t=2![]() ,
,
∴t=1;
(3)当0<t≤1时,S=S△PDQ=![]() DQ×DP=
DQ×DP=![]() ×
×![]() t×t=
t×t=![]() t2,
t2,
当1<t<2时,如图2,
CQ=AQ﹣AC=2AD﹣AC=2![]() t﹣2
t﹣2![]() =2
=2![]() (t﹣1),
(t﹣1),
在Rt△CEQ中,∠CQE=30°,
∴CE=CQtan∠CQE=2![]() (t﹣1)×
(t﹣1)×![]() =2(t﹣1),
=2(t﹣1),
∴S=S△PDQ﹣S△ECQ=![]() ×
×![]() t×t﹣
t×t﹣![]() ×2
×2![]() (t﹣1)×2(t﹣1)=﹣
(t﹣1)×2(t﹣1)=﹣![]() t2+4
t2+4![]() t﹣2
t﹣2![]() ,
,
∴S=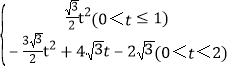 ;
;
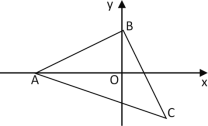
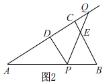
(4)当PQ的垂直平分线过AB的中点F时,如图3,
∴∠PGF=90°,PG=![]() PQ=
PQ=![]() AP=t,AF=
AP=t,AF=![]() AB=2,
AB=2,
∵∠A=∠AQP=30°,
∴∠FPG=60°,
∴∠PFG=30°,
∴PF=2PG=2t,
∴AP+PF=2t+2t=2,
∴t=![]() ;
;
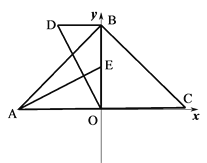
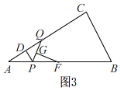
当PQ的垂直平分线过AC的中点M时,如图4,
∴∠QMN=90°,AN=![]() AC=
AC=![]() ,QM=
,QM=![]() PQ=
PQ=![]() AP=t,
AP=t,
在Rt△NMQ中,NQ=![]() ,
,
∵AN+NQ=AQ,
∴![]() +
+![]() =2
=2![]() t,
t,
∴t=![]() ,
,
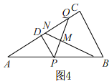
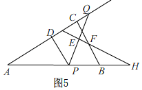
当PQ的垂直平分线过BC的中点时,如图5,
∴BF=![]() BC=1,PE=
BC=1,PE=![]() PQ=t,∠H=30°,
PQ=t,∠H=30°,
∵∠ABC=60°,
∴∠BFH=30°=∠H,
∴BH=BF=1,
在Rt△PEH中,PH=2PE=2t,
∴AH=AP+PH=AB+BH,
∴2t+2t=5,
∴t=![]() ,
,
即:当线段PQ的垂直平分线经过△ABC一边中点时,t的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案