Question

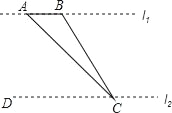
【题目】如图，四边形ABCD是平行四边形，AE平分∠BAD，交DC的延长线于点E，AB=3，EF=0.8，AF=2.4．求AD的长．

Answer 1

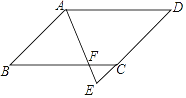
【答案】4

【解析】

由平行四边形的性质得出AB∥CD，则△ABF∽△ECF，由该相似三角形的对应边成比例求得CE=1；由AB∥CD得出内错角相等∠E=∠BAE，再由角平分线等量代换证出∠E=∠DAE，即可得出结论AD=DE=4．

解：∵四边形ABCD为平行四边形，

∴AB=DC=3，AB∥DE，

∴△ABF∽△ECF，

∴ =．

∵AB=3，EF=0.8，AF=2.4，

∴ ，

∴CE=1，

∴DE=DC+CE=3+1=4．

∵AB∥DE，

∴∠BAE=∠E．

∵AE平分∠BAD，

∴∠BAE=∠DAE．

∴∠E=∠DAE．

∴AD=DE=4．

∴AD的长为4．