��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��y����![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C�����κ���y����
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C�����κ���y����![]() +bx+c��ͼ��B��C���㣬����x��ĸ����ύ�ڵ�A��
+bx+c��ͼ��B��C���㣬����x��ĸ����ύ�ڵ�A��
(1)����κ����ı���ʽ��
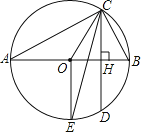
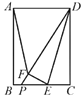
(2)��ͼ1����D�������ߵ��������ϵ�һ���㣬����DC��DB����S��DCB��S��ABCʱ�����D���ꣻ
(3)��ͼ2����(2)�������£���Q��CA���ӳ����ϣ�����DQ��AD������Q��QP��y�ᣬ����������P������AQD����ACO+��ADC�������PQ�ij���
���𰸡���1��![]() ����2��
����2��![]() ����3��6
����3��6
��������
��1�������B��C�����꣬Ȼ�������κ����Ľ���ʽ���ⷽ���鼴�ɣ�
(2)��D��DG��x����G����C��CF��DG��F����B��BE��CF��E����D��x��y������x��0��y��0�����S��ABC������S��CBD=S��CDF��S��CEB��S����EBDF�ⷽ�̽�õ�x��ֵ���Ӷ��õ�D��������
(3)����AD����D��DM��x����M�������ֱ��CD�Ľ���ʽΪy=��x+2���õ�CO=OR=2�����ORC=45�㣮��֤����AQD=45�㣮ͨ�����ɶ������涨���õ�AC2+AD2= DC2�����С�CAD=90�㣬�Ӷ��С�AQD�ǵ���ֱ�����������ɵ��������ε����ʵõ�AQ=AD��ͨ��֤����QAN�ա�ADM���õ�NA��QN�ij��������õ�ON=4�����ɵõ�N����4��0������P�������Ϊx=-4��������κ������ɵõ�y��ֵ���Ӷ��õ����ۣ�
��1����![]() �У���y=0����ã�x=4����B(4��0)����x=0���ã�y=2����C(0��2)����B(4��0)��C(0��2)����
�У���y=0����ã�x=4����B(4��0)����x=0���ã�y=2����C(0��2)����B(4��0)��C(0��2)����![]() �У��ã�
�У��ã�![]() ����ã�
����ã�![]() ������κ����ı���ʽΪ��
������κ����ı���ʽΪ��![]() ��
��
(2)��D��DG��x����G����C��CF��DG��F����B��BE��CF��E����D��x��y����
��D�ڵ�����������x��0��y��0��
��B��4��0����C(0��2)����CE=OB=4��CO=BE=FG=2��EF=BG=x-4��DF=DG+FG=2-y��S��ABC=![]() AB��OC=
AB��OC=![]() ����4+1����2=5��
����4+1����2=5��
S��CBD=S��CDF��S��CEB��S����EBDF=![]() ���������x+2y=��1��
���������x+2y=��1��
��D��x��y���ڶ��κ���![]() ������
������![]() ���������
���������![]() ���ࣨx��5����x+1��=0����x=5��x=��1����ȥ����
���ࣨx��5����x+1��=0����x=5��x=��1����ȥ����
��x=5ʱ��y=![]() =��3����D��5����3����
=��3����D��5����3����
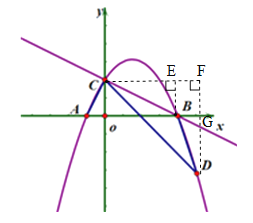
(3)��ͼ������AD����D��DM��x����M����ֱ��CD�Ľ���ʽΪy=kx+b����C��0��2����D��5����3������õ���![]() �������
�������![]() ����ֱ��CD�Ľ���ʽΪy=��x+2����y=0�������x=2����R(2��0)����CO=OR=2�����ORC=45�㣮
����ֱ��CD�Ľ���ʽΪy=��x+2����y=0�������x=2����R(2��0)����CO=OR=2�����ORC=45�㣮
�ߡ�ACO+��CAO=90�㣬��CAO+��OAD=90�㣬���ACO=��OAD�����ACO+��ADC=��OAD+��ADC=��ARC=45�㣬���AQD=45�㣮
��AC2=12+22=5��AD2=(5+1)2+32=45��DC2=52+(2+3)2=50����AC2+AD2=5+45=50= DC2�����CAD=90�㣬���QAD=90�㣮
�ߡ�AQD=45�㣬���AQD�ǵ���ֱ������������AQ=AD��
�ߡ�QAD=90�㣬���NAQ+��DAM=90�㣮
�ߡ�NAQ+��AQN=90�㣬���AQN=��MAD���ڡ�QAN�͡�ADM�У�����AQN=��MAD����QNA=��AMD=90�㣬AQ=AD�����QAN�ա�ADM����NA=DM=3��QN=AM=6����ON=4����N����4��0������P��x��y����
��QP��y�ᣬ��P�������Ϊx=-4����y=![]() =��12����PN=12����PQ=PN-QN=12��6=6��
=��12����PN=12����PQ=PN-QN=12��6=6��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�