题目内容
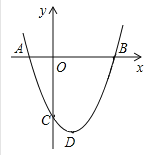
【题目】已知如图，抛物线的顶点D的坐标为（1，-4），且与y轴交于点
C（0，3）
求该函数的关系式；
求改抛物线与x轴的交点A，B的坐标.
【答案】（1）
（2）A（3，0），B（-1，0）.
【解析】试题分析：（1）由抛物线的顶点D的坐标为（1，-4），可设抛物线的函数关系式为y=a（x-1）2-4，再将C（0，-3）代入求解即可；
（2）将y=0代入（1）中所求解析式，得到x2-2x-3=0，解方程求出x的值，进而得到抛物线与x轴的交点A，B的坐标．
试题解析：（1）∵抛物线的顶点D的坐标为(1，4)，
∴设抛物线的函数关系式为y=a(x1)24，
又∵抛物线过点C(0，3)，
∴3=a(01)24，
解得a=1，
∴抛物线的函数关系式为y=(x1)24，
即y=x22x3；
（2）令y=0，得：x2
，
解得
， 
.
所以坐标为A（3，0），B（-1，0）.
练习册系列答案
名校课堂系列答案
相关题目
