Question

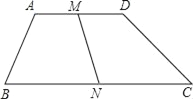
【题目】如图，E、F分别是 四边形ABCD的边AB、CD上的点，AF与DE相交于点P，BF与CE相交于点Q，记S1＝S△APD，S2＝S△BQC，四边形EQFP的面积为S．

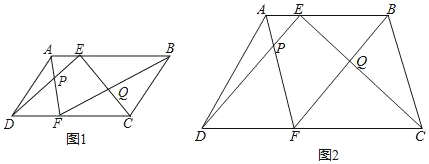
（1）若四边形ABCD为平行四边形，如图1，求证：S＝S1+S2；

（2）若四边形ABCD为一般凸多边形，AB∥CD，如图2，求证：S＝S1+S2．

Answer 1

【答案】（1）证明见解析 （2）证明见解析

【解析】

（1）连接EF两点，由三角形的面积公式我们可以推出S△EFC＝S△BCF，S△EFD＝S△ADF，所以S△EFG＝S△BCQ，S△EFP＝S△ADP，因此可以推出阴影部分的面积就是S△APD+S△BQC．

（2）连接EF，证明方法类似；

证明：（1）连接E、F两点，

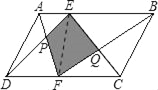
∵四边形ABCD是平行四边形，

∴AB∥CD，

∴△EFC的FC边上的高与△BCF的FC边上的高相等，

∴S△EFC＝S△BCF，

∴S△EFQ＝S△BCQ，

同理：S△EFD＝S△ADF，

∴S△EFP＝S△ADP，

∴S＝S1+S2．

（2）连接EF．

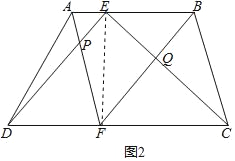
∵AB∥CD，

∴△EFC的FC边上的高与△BCF的FC边上的高相等，

∴S△EFC＝S△BCF，

∴S△EFQ＝S△BCQ，

同理：S△EFD＝S△ADF，

∴S△EFP＝S△ADP，

∴S＝S1+S2．