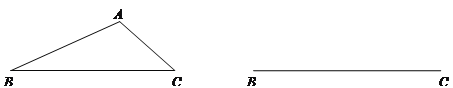题目内容

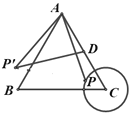
【题目】如图，等边三角形ABC中，AB=4cm，以C为圆心，1cm长为半径画⊙C，点P在⊙C上运动，连接AP，并将AP绕点A顺时针旋转60°至AP′，点D是边AC的中点，连接DP′.在点P移动的过程中，线段DP′长度的最小值为______cm.

【答案】

【解析】

通过画图发现P′的运动路线是以B为圆心，以1cm为半径的圆，连接BD，由“三线合一”可得BD⊥AC，则当点P′在BD上时，DP′最小，利用勾股定理求得BD的长，即可求得DP′的长.

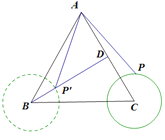
解：如图以B为圆心，1cm长为半径画⊙B，连接BD，

当点P′在BD上时，DP′最小，

∵△ABC是等边三角形，D是AC中点，AB=4cm，

∴BD⊥AC，AD=2cm，

∴cm，

∴DP′=BD﹣BP′=cm.

故答案为：.

练习册系列答案
相关题目

【题目】如图，已知△ABC（AC＜AB＜BC），请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：

（1）在边BC上确定一点P，使得PA+PC=BC；

（2）作出一个△DEF，使得：①△DEF是直角三角形；②△DEF的周长等于边BC的长。

【题目】如图，已知正方形的边长为4，是边上的一个动点，连接，过点作的垂线交于点，以为边作正方形，顶点在线段上，对角线，相交于点.

（1）若，则 ；

（2）①求证：点一定在的外接圆上；

②当点从点运动到点时，点也随之运动，求点经过的路径长；

（3）在点从点到点的运动过程中，的外接圆的圆心也随之运动，求该圆心到边的距离的最大值.

【题目】某景区在距离地面米的悬崖点处垂直水平线搭建了一个悬崖秋千，秋千拉绳均由钢管制作而成，当游客乘坐该秋千时，机器会将秋千拉至最高接近与地面平行的点处(此时) ，然后放下．该悬崖秋千以其惊险刺激立即成为网红打卡地．

若秋千放下秒后点的垂直距离为米，求秋千拉绳的长；

若某一时刻秋千荡至与点水平距离相距米的点处，求的度数，并求此时秋千底端距离悬崖底部多少米(结果保留整数参考数据：)

【题目】如图1，在平面直角坐标系中，抛物线yx2bxc交x轴于点A，B，点B的坐标为(4，0)，与y轴于交于点C(0，﹣2)．

（1）求此抛物线的解析式；

（2）在抛物线上取点D，若点D的横坐标为5，求点D的坐标及∠ADB的度数；

（3）在（2）的条件下，设抛物线对称轴交x轴于点H，△ABD的外接圆圆心为M（如图1），

①求点M的坐标及⊙M的半径；

②过点B作⊙M的切线交于点P（如图2），设Q为⊙M上一动点，则在点Q运动过程中的值是否变化？若不变，求出其值；若变化，请说明理由．

【题目】如图，在矩形ABCD中，点E，F分别在边AD，DC上，AB=6，DF＝4，将矩形沿直线EF折叠，点D恰好落在BC边上的点G处，连接DG交EF于点H.

(1)求DE的长度.

(2)求的值.

(3)若AB边上有且只存在2个点P，使△APE与△BPG相似，请直接写出边AD的值.

【题目】如图，二次函数y＝x2+bx﹣3的图象与x轴分别相交于A、B两点，点B的坐标为（3，0），与y轴的交点为C，动点T在射线AB上运动，在抛物线的对称轴l上有一定点D，其纵坐标为2，l与x轴的交点为E，经过A、T、D三点作⊙M．

（1）求二次函数的表达式；

（2）在点T的运动过程中，

①∠DMT的度数是否为定值？若是，请求出该定值：若不是，请说明理由；

②若MT＝AD，求点M的坐标；

（3）当动点T在射线EB上运动时，过点M作MH⊥x轴于点H，设HT＝a，当OH≤x≤OT时，求y的最大值与最小值（用含a的式子表示）．

【题目】由边长相等的小正方形组成的网格，以下各图中点A、B、C、D都在格点上．

（1）在图1中，PC：PB=　 　；

（2）利用网格和无刻度的直尺作图，保留痕迹，不写作法．

①如图2，在AB上找点P，使得AP：PB=1：3；

②如图3，在BC上找点P，使得△APB∽△DPC；

③如图4，在△ABC中内找一点P，连接PA、PB、PC，将△ABC分成面积相等的三部分．

【题目】如图，将一个小球从斜坡的点O处抛出，小球的抛出路线可以用二次函数y＝4x－x2刻画，斜坡可以用一次函数y＝x刻画，下列结论错误的是( )

A.斜坡的坡度为1: 2

B.小球距O点水平距离超过4米呈下降趋势

C.小球落地点距O点水平距离为7米

D.当小球抛出高度达到7.5m时，小球距O点水平距离为3m

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网