题目内容
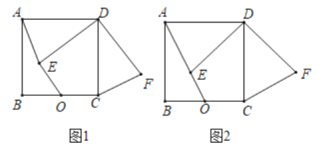
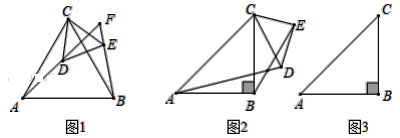
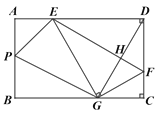
【题目】如图,在矩形ABCD中,点E,F分别在边AD,DC上,AB=6,DF=4,将矩形沿直线EF折叠,点D恰好落在BC边上的点G处,连接DG交EF于点H.
(1)求DE的长度.
(2)求![]() 的值.
的值.
(3)若AB边上有且只存在2个点P,使△APE与△BPG相似,请直接写出边AD的值.
【答案】(1)![]() ;(2)3;(3)
;(2)3;(3)![]() 或
或![]() .
.
【解析】
(1)根据矩形的性质易得CF=2,由折叠的性质可得DF=GF,在Rt△CFG中,利用勾股定理求得CG=![]() ,在Rt△CDG中求得DG=
,在Rt△CDG中求得DG=![]() ,得到∠CDG=30°,即∠EDG=60°,则可得△EDG为等边三角形,得到DE=DG=
,得到∠CDG=30°,即∠EDG=60°,则可得△EDG为等边三角形,得到DE=DG=![]() ;
;
(2)根据折叠的性质可得EF垂直平分DG,在Rt△DHF中,根据直角三角形中30°角所对直角边为斜边的一半得到HF=2,在Rt△DEF中,求得EF的值,进而得到EH的值,即可得到答案;
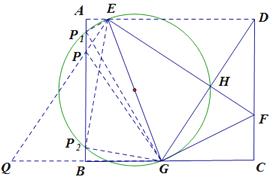
(3)如图,
(1)由折叠的性质可得DF=GF,DE=GE,
∵AB=6,DF=4,
∴CF=CD﹣DF=AB﹣DF=2,
在Rt△CFG中,![]() ,
,
在Rt△CDG中,![]() ,
,
∴DG=2CG,
∴∠CDG=30°,
∴∠EDG=60°,
∴△EDG为等边三角形,
∴DE=DG=![]() ;
;
(2)由折叠的性质可得:EF垂直平分DG,
∵∠CDG=30°,
∴HF=![]() DF=2,
DF=2,
∵∠DEG=60°,
∴∠DEF=30°,
∴EF=2DF=8,
∴EH=EF﹣HF=6,
∴![]() ;
;
(3)如图,作G点关于AB的对称点Q,连接EQ交AB于P,此时△APE∽△BPG,以EG为直径作圆交AB于P1,P2,此时△AP1E∽△BP1G,△AP2E∽△BP2G,
①当P点与P1重合时,满足条件,易证AP=AE,BP=BG,
设AD=x,则AP=AE=x﹣![]() ,BG=BP=6+
,BG=BP=6+![]() ﹣x,
﹣x,
则DE=2(BG﹣AE),即![]() ,
,
解得a=![]() ;
;
②当P1与P2重合时,满足条件,此时以GE为直径的圆与AB相切,
设AE=m,BG=n,
则DE=2(n﹣m)=![]() ,GE=2×
,GE=2×![]() =
=![]() ,
,
整理解得m=![]() ,
,
∴AD=AE+DE=![]() .
.
综上可得AD的值为![]() 或
或![]() .
.

 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
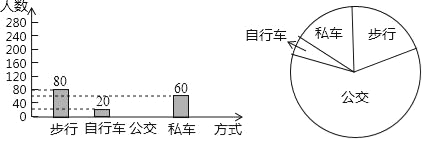
出彩同步大试卷系列答案【题目】在学校组织的“文明出行”知识竞赛中,8(1)和8(2)班参赛人数相同,成绩分为A、B、C三个等级,其中相应等级的得分依次记为A级100分、B级90分、C级80分,达到B级以上(含B级)为优秀,其中8(2)班有2人达到A级,将两个班的成绩整理并绘制成如下的统计图,请解答下列问题:

(1)求各班参赛人数,并补全条形统计图;
(2)此次竞赛中8(2)班成绩为C级的人数为_______人;
(3)小明同学根据以上信息制作了如下统计表:
平均数(分) | 中位数(分) | 方差 | |
8(1)班 | m | 90 | n |
8(2)班 | 91 | 90 | 29 |
请分别求出m和n的值,并从优秀率和稳定性方面比较两个班的成绩;