题目内容
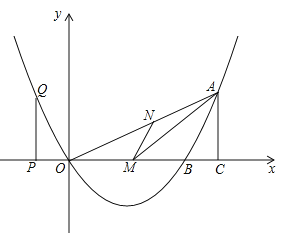
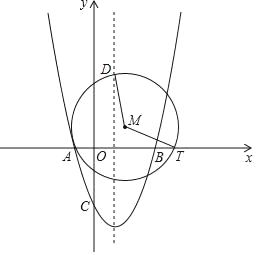
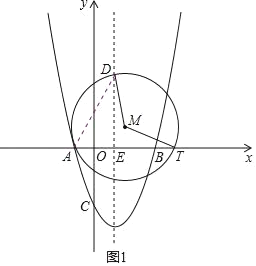
【题目】如图，二次函数y＝x2+bx﹣3的图象与x轴分别相交于A、B两点，点B的坐标为（3，0），与y轴的交点为C，动点T在射线AB上运动，在抛物线的对称轴l上有一定点D，其纵坐标为2
，l与x轴的交点为E，经过A、T、D三点作⊙M．
（1）求二次函数的表达式；
（2）在点T的运动过程中，
①∠DMT的度数是否为定值？若是，请求出该定值：若不是，请说明理由；
②若MT＝
AD，求点M的坐标；
（3）当动点T在射线EB上运动时，过点M作MH⊥x轴于点H，设HT＝a，当OH≤x≤OT时，求y的最大值与最小值（用含a的式子表示）．
【答案】（1）y＝x2﹣2x﹣3（2）①在点T的运动过程中，∠DMT的度数是定值②（0，
）（3）见解析
【解析】
（1）把点B的坐标代入抛物线解析式求得系数b的值即可；
（2）①如图1，连接AD．构造Rt△AED，由锐角三角函数的定义知，tan∠DAE＝．即∠DAE＝60°，由圆周角定理推知∠DMT＝2∠DAE＝120°；
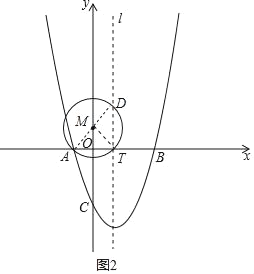
②如图2，由已知条件MT＝
AD，MT＝MD，推知MD＝AD，根据△ADT的外接圆圆心M在AD的中垂线上，得到：点M是线段AD的中点时，此时AD为⊙M的直径时，MD＝AD．根据点A、D的坐标求得点M的坐标即可；
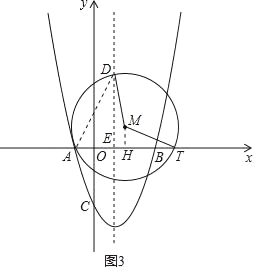
（3）如图3，作MH⊥x于点H，则AH＝HT＝AT．易得H（a﹣1，0），T（2a﹣1，0）．由限制性条件OH≤x≤OT、动点T在射线EB上运动可以得到：0≤a﹣1≤x≤2a﹣1．
需要分类讨论：（i）当
，即
，根据抛物线的增减性求得y的极值．
（ii）当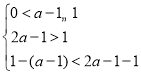
，即
＜a≤2时，根据抛物线的增减性求得y的极值．
（iii）当a﹣1＞1，即a＞2时，根据抛物线的增减性求得y的极值．
解：（1）把点B（3，0）代入y＝x2+bx﹣3，得32+3b﹣3＝0，
解得b＝﹣2，
则该二次函数的解析式为：y＝x2﹣2x﹣3；
（2）①∠DMT的度数是定值．理由如下：
如图1，连接AD．
∵抛物线y＝x2﹣2x﹣3＝（x﹣1）2﹣4．
∴抛物线的对称轴是直线x＝1．
又∵点D的纵坐标为2，
∴D（1，2）．
由y＝x2﹣2x﹣3得到：y＝（x﹣3）（x+1），
∴A（﹣1，0），B（3，0）．
在Rt△AED中，tan∠DAE＝
．
∴∠DAE＝60°．
∴∠DMT＝2∠DAE＝120°．
∴在点T的运动过程中，∠DMT的度数是定值；
②如图2，∵MT＝AD．又MT＝MD，
∴MD＝AD．
∵△ADT的外接圆圆心M在AD的中垂线上，
∴点M是线段AD的中点时，此时AD为⊙M的直径时，MD＝AD．
∵A（﹣1，0），D（1，2），
∴点M的坐标是（0，）．
（3）如图3，作MH⊥x于点H，则AH＝HT＝AT．
又HT＝a，
∴H（a﹣1，0），T（2a﹣1，0）．
∵OH≤x≤OT，又动点T在射线EB上运动，
∴0≤a﹣1≤x≤2a﹣1．
∴0≤a﹣1≤2a﹣1．
∴a≥1，
∴2a﹣1≥1．
（i）当，即1
时，
当x＝a﹣1时，y最大值＝（a﹣1）2﹣2（a﹣1）﹣3＝a2﹣4a；
当x＝1时，y最小值＝4．
（ii）当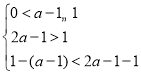，即＜a≤2时，
当x＝2a﹣1时，y最大值＝（2a﹣1）2﹣2（2a﹣1）﹣3＝4a2﹣8a．
当x＝1时，y最小值＝﹣4．
（iii）当a﹣1＞1，即a＞2时，
当x＝2a﹣1时，y最大值＝（2a﹣1）2﹣2（2a﹣1）﹣3＝4a2﹣8a．
当x＝a﹣1时，y最小值＝（a﹣1）2﹣2（a﹣1）﹣3＝a2﹣4a．
