题目内容
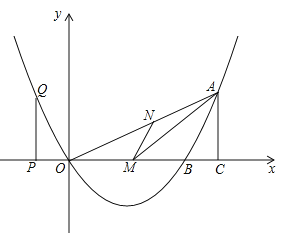
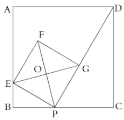
【题目】如图,已知正方形![]() 的边长为4,
的边长为4,![]() 是边
是边![]() 上的一个动点,连接
上的一个动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,顶点
,顶点![]() 在线段
在线段![]() 上,对角线
上,对角线![]() ,
,![]() 相交于点
相交于点![]() .
.

(1)若![]() ,则
,则![]() ;
;
(2)①求证:点![]() 一定在
一定在![]() 的外接圆上;
的外接圆上;
②当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,求点
也随之运动,求点![]() 经过的路径长;
经过的路径长;
(3)在点![]() 从点
从点![]() 到点
到点![]() 的运动过程中,
的运动过程中,![]() 的外接圆的圆心也随之运动,求该圆心到边
的外接圆的圆心也随之运动,求该圆心到边![]() 的距离的最大值.
的距离的最大值.
【答案】(1)![]() ;(2)①详见解析;②2
;(2)①详见解析;②2![]() ;(3)
;(3)![]()
【解析】
(1)由正方形的性质得出∠C=∠B=∠EPG=90°,PF⊥EG,CD=BC=4,∠OEP=45°,由角的互余关系证出∠BEP=∠DPC,得出△CDP∽△BPE,得出对应边成比例即可求出BE的长;
(2)①B、P、O、E四点共圆,即可得出结论;
②连接BO、BD,由勾股定理求出BD=4![]() ,由圆周角定理得出∠OBP=∠OEP=45°,周长点O在BD上,当P运动到点C时,O为BD的中点,即可得出答案;
,由圆周角定理得出∠OBP=∠OEP=45°,周长点O在BD上,当P运动到点C时,O为BD的中点,即可得出答案;
(3)设![]() 的外接圆的圆心为M,作MN⊥CB于N,由三角形中位线定理得出MN=
的外接圆的圆心为M,作MN⊥CB于N,由三角形中位线定理得出MN=![]() BE,设BP=x,则CP=4-x,由相似三角形的对应边成比例求出BE=x-
BE,设BP=x,则CP=4-x,由相似三角形的对应边成比例求出BE=x-![]() x2=-
x2=-![]() (x-2)2+1,由二次函数的最大值求出BE的最大值为1,得出MN的最大值=
(x-2)2+1,由二次函数的最大值求出BE的最大值为1,得出MN的最大值=![]() 即可.
即可.
解:(1)∵四边形ABCD、四边形PEFG是正方形,
∴∠C=∠B=∠EPG=90°,PF⊥EG,CD=BC=4,∠OEP=45°,
∴∠BEP+∠BPE=90°,∠DPC+∠BPE=90°,
∴∠BEP=∠DPC,
∴△CDP∽△BPE;
∴![]() ,即
,即![]()
∴BE=![]()
(2)①证明:如图,
取PE的中点Q,连接BQ,OQ,
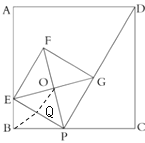
∵∠POE=90°,
∴OQ=![]() PE,
PE,
∵△BPE是直角三角形,
∴点Q是Rt△BPE外接圆的圆心,
∴BQ=![]() PE,
PE,
∴OQ=BQ,
∴点O一定在△APE的外接圆上;(到圆心的距离等于半径的点必在此圆上)
②解:连接OB、BD,如图所示:
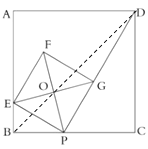
∵四边形ABCD是正方形,
∴∠ABC=90°,∠DBC=45°,
∴BD=![]() =4
=4![]() ,
,
∵B、P、O、E四点共圆,
∴∠OBP=∠OEP=45°,
∴点O在BD上,
当P运动到点C时,O为BD的中点,OB=![]() BD=2
BD=2![]() ,
,
即点O经过的路径长为2![]() ;
;
(3)解:设△BPE的外接圆的圆心为M,作MN⊥BC于N,如图:
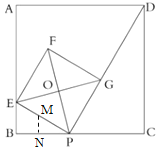
则MN∥BE,
∵ME=MP,
∴BN=PN,
∴MN=![]() BE,
BE,
设BP=x,则PC=4-x,
由(1)得:△CDP∽△BPE,
∴![]() ,即
,即![]() ,
,
解得:BE=x-![]() x2=-
x2=-![]() (x-2)2+1
(x-2)2+1
∴x=2时,BE的最大值为1,此时MN的值最大=![]() ,
,
即△APE的圆心到BC边的距离的最大值为![]() .
.