��Ŀ����
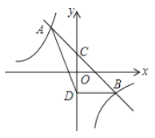
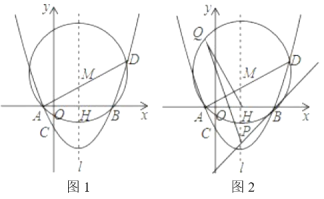
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y![]() x2bxc��x���ڵ�A��B����B������Ϊ(4��0)����y���ڽ��ڵ�C(0����2)��
x2bxc��x���ڵ�A��B����B������Ϊ(4��0)����y���ڽ��ڵ�C(0����2)��
��1����������ߵĽ���ʽ��
��2������������ȡ��D������D�ĺ�����Ϊ5�����D�����꼰��ADB�Ķ�����
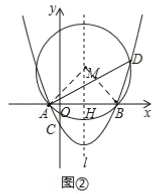
��3���ڣ�2���������£��������߶Գ���![]() ��x���ڵ�H����ABD�����ԲԲ��ΪM����ͼ1����
��x���ڵ�H����ABD�����ԲԲ��ΪM����ͼ1����
�����M�����꼰��M�İ뾶��
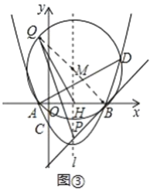
�ڹ���B����M�����߽�![]() �ڵ�P����ͼ2������QΪ��M��һ���㣬���ڵ�Q�˶�������
�ڵ�P����ͼ2������QΪ��M��һ���㣬���ڵ�Q�˶�������![]() ��ֵ�Ƿ�仯�������䣬�����ֵ�����仯����˵�����ɣ�
��ֵ�Ƿ�仯�������䣬�����ֵ�����仯����˵�����ɣ�
���𰸡���1��![]() ����2����
����2����![]() ������Ϊ
������Ϊ![]() ��45������3���ٵ�
��45������3���ٵ�![]() ������Ϊ
������Ϊ![]() ��
��![]() �İ뾶Ϊ
�İ뾶Ϊ![]() �����ڵ�
�����ڵ�![]() �˶�������
�˶�������![]() ��ֵ���䣬��ֵΪ
��ֵ���䣬��ֵΪ![]()
��������
��1����![]() ��
��![]() �������ʽ���������ʽ��ϵ�������ɵý⣻
�������ʽ���������ʽ��ϵ�������ɵý⣻
��2����![]() �������ʽ�����
�������ʽ�����![]() ���ɵ�
���ɵ�![]() �����ꣻ��
�����ꣻ��![]() �����A��B���꣬�ɹ��ɶ������������빫ʽ���AD��BD��������������BH���Ӷ������ADB������ֵ����֪��ADB�Ķ�����
�����A��B���꣬�ɹ��ɶ������������빫ʽ���AD��BD��������������BH���Ӷ������ADB������ֵ����֪��ADB�Ķ�����
��3������Բ�ܽǶ�����ϵ���ֱ�������αߵĹ�ϵ�����![]() ���������
���������![]() �İ뾶����֤��QH��QP���ڵġ�HMQ�͡�QMP���Ƽ��ɣ�
�İ뾶����֤��QH��QP���ڵġ�HMQ�͡�QMP���Ƽ��ɣ�
��1����![]() ��
��![]() �������ʽ�ã�
�������ʽ�ã�![]() ��
��![]() ��
��
���������ߵĽ���ʽΪ��![]()
��2����![]() ʱ��
ʱ��![]()
����![]() ������Ϊ
������Ϊ![]() ��
��
��![]() ʱ��
ʱ��![]() ��4��
��4��
��![]() ��
��![]()
��ͼ������![]() ����
����![]() ��
��![]() ��
��

��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��3������ͼ������![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
����![]() ������Ϊ
������Ϊ![]() ����
����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ��
��
����ͼ������![]() ��
��![]() ��
��
������![]() ����
����![]() �����߽�
�����߽�![]() �ڵ�
�ڵ�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��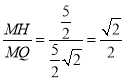 ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
�� ��
��
���ڵ�![]() �˶�������
�˶�������![]() ��ֵ���䣬��ֵΪ
��ֵ���䣬��ֵΪ![]() ��
��