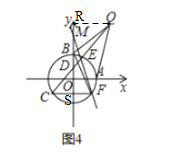题目内容
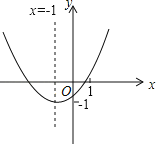
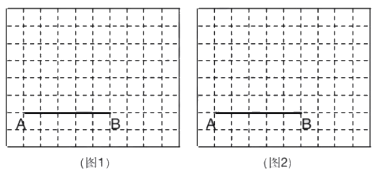
【题目】如图1,在平面直角坐标系![]() 中,半径为1的
中,半径为1的![]() 与
与![]() 轴正半轴和
轴正半轴和![]() 轴正半轴分别交于
轴正半轴分别交于![]() 两点,直线
两点,直线![]() :
:![]() 与
与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 两点.
两点.

(l)当直线![]() 与
与![]() 相切时,求出点
相切时,求出点![]() 的坐标和点
的坐标和点![]() 的坐标;
的坐标;
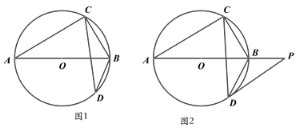
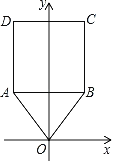
(2)如图2,当点![]() 在线段
在线段![]() 上时,直线
上时,直线![]() 与
与![]() 交于
交于![]() 两点(点
两点(点![]() 在点
在点![]() 的上方),过点
的上方),过点![]() 作
作![]() 轴,与
轴,与![]() 交于另一点
交于另一点![]() ,连结
,连结![]() 交
交![]() 轴于点
轴于点![]() .
.
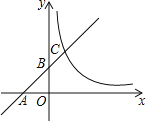
①如图3,若点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的长并写出解答过程;
的长并写出解答过程;
②如图2,若点![]() 与点
与点![]() 不重合时,
不重合时,![]() 的长是否发生变化,若不发生变化,请求出
的长是否发生变化,若不发生变化,请求出![]() 的长并写出解答过程;若发生变化,请说明理由.
的长并写出解答过程;若发生变化,请说明理由.
(3)如图4,在(2)的基础上,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到
到![]() ,若点
,若点![]() 在
在![]() 的延长线时,请用等式直接表示线段
的延长线时,请用等式直接表示线段![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1)点![]() 和点
和点![]() 的坐标是
的坐标是![]() ,
,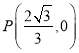 ;(2)①
;(2)①![]() ;②不发生变化,
;②不发生变化,![]() 的长为
的长为![]() ,理由详见解析;(3)
,理由详见解析;(3)![]() ,理由详见解析
,理由详见解析
【解析】
(1)由已知可得点M坐标及点![]() 在原点
在原点![]() 的右侧,设直线
的右侧,设直线![]() 与
与![]() 相切于点
相切于点![]() ,连结
,连结![]() ,则
,则![]() ,易证
,易证![]() ,根据相似三角形的性质即可求出OP的值,从而得出点P的坐标;
,根据相似三角形的性质即可求出OP的值,从而得出点P的坐标;
(2)①由点![]() 与点
与点![]() 重合得出
重合得出![]() ,易证
,易证![]() ,根据相似三角形的性质即可求出OD的值;
,根据相似三角形的性质即可求出OD的值;
②过点![]() 作
作![]() 的直径
的直径![]() ,连结
,连结![]() ,
,![]() ,根据同角的余角相等及等边对等角可得
,根据同角的余角相等及等边对等角可得![]() ,最后根据相似三角形的性质即可求出OD的值;
,最后根据相似三角形的性质即可求出OD的值;
(3)在(2)的基础上有![]() 可直接使用,由旋转
可直接使用,由旋转![]() 联想到构造三垂直全等模型,作QR
联想到构造三垂直全等模型,作QR![]()
![]() 轴,即能用F的坐标表示QR、BR等线段长度,又由
轴,即能用F的坐标表示QR、BR等线段长度,又由![]() 得相似,对应边的比相等得到用F坐标表示的等式,利用F在
得相似,对应边的比相等得到用F坐标表示的等式,利用F在![]() 上化简式子,并代入求
上化简式子,并代入求![]() ,即能得到
,即能得到![]() 与
与![]() 的长度关系.
的长度关系.
解:(1)如图1,
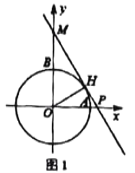
∵![]() 与
与![]() 轴交于
轴交于![]() 点,
点,
∴当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为
的坐标为![]()
∵![]() 与
与![]() 轴交于
轴交于![]() 点,
点,
∴点![]() 在原点
在原点![]() 的右侧.
的右侧.
设直线![]() 与
与![]() 相切于点
相切于点![]() ,连结
,连结![]() ,则
,则![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 和点
和点![]() 的坐标是
的坐标是![]() ,
,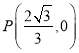
(2)①如图2,
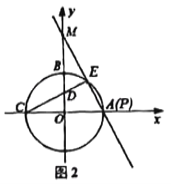
∵点![]() 与点
与点![]() 重合,
重合,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
②不发生变化,![]() 的长为
的长为![]() ,理由如下:
,理由如下:
过点![]() 作
作![]() 的直径
的直径![]() ,连结
,连结![]() ,
,![]() ,
,
∴![]()
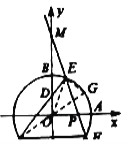
∵![]() 轴,
轴,
∴![]() 轴
轴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
(3)![]()
过点Q作QR![]()
![]() 轴与R,设CF与
轴与R,设CF与![]() 轴交点为S
轴交点为S
![]()
![]() 线段BF绕点B逆时针旋转
线段BF绕点B逆时针旋转![]() 到BQ
到BQ
![]() ,BQ=BF,
,BQ=BF,
即![]() 是等腰直角三角形
是等腰直角三角形
![]()
![]()
在![]() 和
和![]() 中
中
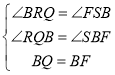
![]()
![]()
设![]() ,
,![]()
则![]()
![]() 在(2)的基础上有
在(2)的基础上有![]()
![]()
![]() ,C、D、Q在同一直线上
,C、D、Q在同一直线上
![]()
![]()
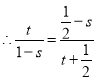
整理得:![]()
![]() 点
点![]() 在
在![]() 上,满足
上,满足![]()
代入整理得:![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()