题目内容
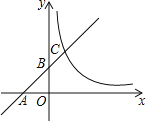
【题目】如图,![]() (b为常数)的图象与x轴,y轴分别交于点A,B与反比例函数
(b为常数)的图象与x轴,y轴分别交于点A,B与反比例函数![]() (x>0)的图象交于点C.若ACBC=4,则k的值为_____.
(x>0)的图象交于点C.若ACBC=4,则k的值为_____.
【答案】2
【解析】
作CD⊥x轴于D,先求出y=x+b(b为常数)的图象与x轴,y轴分别交于点A,B两点坐标,根据勾股定理得出AB,再根据C(x,x+b),△ADC也是等腰直角三角形,求出AC, 再根据ACBC=4,得出x(x+b)的值即可.
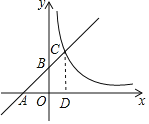
解:作CD⊥x轴于D,则OB∥CD,ADC=90,
∵y=x+b(b为常数)的图象与x轴,y轴分别交于点A,B,
∴A(-b,0),B(0,b),
∴OA=OB=b,∴AB=![]() b;
b;
∵△AOB是等腰直角三角形,OB∥CD,
∴△ADC也是等腰直角三角形,
∴AD=CD,∴C(x,x+b),
∴k=x(x+b),且AC=![]() (x+b)
(x+b)
∵ACBC=4,∴![]() (x+b)
(x+b)![]() b=4;
b=4;
∴x(x+b)=2 ∴k=2
故答案为2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目