题目内容
【题目】某校开展学生对食堂评价调查,每名学生只能从“优”、“良”、“差”三种选择其中一个进行评价,假设这三种评价是等可能的且所有学生都参与了评价.学校对学生的评价信息进行了统计,并绘制了两幅不完整的统计图,利用图中所提供的信息解决下面问题:

(1)学校共有多少学生参与评价?
(2)图2中“良”所占扇形圆心角的度数是________;
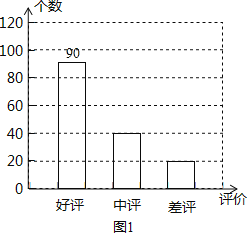
(3)请将图1补充完整;
(4)若甲、乙两名学生参与了对食堂的评价,请你用列表格或画树状图的方法求两人中至少有一个给“差”评价的概率.
【答案】(1)150人;(2)96°;(3)见解析;(4)列表见解析,![]()
【解析】
(1)用中评和差评的人数之和除以它们所占的百分比得到调查的总人数;
(2)用360°乘以“良”所占的百分比得到图2中“良”所占扇形圆心角的度数;
(3)计算出“好评”的人数,然后补全条形统计图;
(4)画树状图展示所有9种等可能的结果数,找出两人中至少有一个给“差”评价的结果数,然后概率公式求解.
解:(1)学校参与评价的学生一共有:![]() (个);
(个);
(2)360×![]() =96°,
=96°,
所以图2中“良”所占扇形圆心角的度数是96°,
故答案为96°;
(3)“好评”的人数为60%×150=90(人),
图1补充为:
(4)列表如下:
优 | 良 | 差 | |
优 | 优,优 | 优,良 | 优,差 |
良 | 良,优 | 良,良 | 良,差 |
差 | 差,优 | 差,良 | 差,差 |
由表可知,一共有![]() 种等可能结果,其中至少有一个给“差”的有
种等可能结果,其中至少有一个给“差”的有![]() 种,
种,
![]() 两人中至少有一个给“差”的概率是
两人中至少有一个给“差”的概率是![]() .
.

练习册系列答案
相关题目