Question

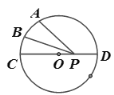
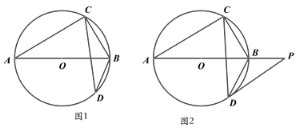
【题目】已知AB是⊙O的的直径，弦CD与AB相交，∠BCD=25°。

（1）如图1，求∠ABD的大小；

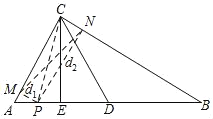
（2）如图2，过点D作O的切线，与AB的延长线交于点P，若DP∥AC，求∠OCD的度数。

Answer 1

【答案】（1）∠ABD=65°；

（2）∠OCD=25°.

【解析】

（1）根据直径所对的圆周角是90°可得∠ACB=90°，由已知∠BCD=25°，继而可求∠ACD，再由圆周角定理可得∠ABD=∠ACD；

（2）连接OD，根据切线的性质可得∠ODP=90°，根据圆周角定理可得∠DOB=2∠DCB=50°，然后根据三角形内角和定理可得∠P=40°，再由平行线的性质可得∠P=∠OAC=40°，再由三角形的外角和定理求得∠COB=80°，再由等腰三角形的性质求得∠OCD即可.

解：∵AB是直径，

∴∠ACB=90°，

又∵∠BCD=25°，

∴∠ACD=65°，

∵∠ACD=∠ABD，

∴∠ABD=65°；

（2）如图：

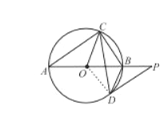
连接OD，

∵DP是⊙O的切线，

∴∠ODP=90°，

∵∠DOB=2∠DCB，

∴∠DOB=2×25°=50°，

∴∠P=40°，

∵AC∥DP，

∴∠OAC=∠P=40°，

∴∠COB=∠OAC+∠OCA=80°，

∴∠COD=∠COB+∠DOB=130°，

∵CO=DO，

∴∠OCD=∠ODC=25°.