Question

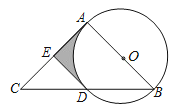
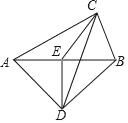
【题目】如图，把一副三角板按如图放置，∠ACB＝∠ADB＝90°，∠CAB＝30°，∠DAB＝45°，点E是AB的中点，连结CE，DE，DC．若AB＝8，则△DEC的面积为_____．

Answer 1

【答案】4

【解析】

作CF⊥DE交DE的延长线于F，根据直角三角形斜边中线的性质得出DE＝CE＝AE＝BE＝AB＝4，然后根据∠CAB＝30°，∠DAB＝45°，得出△BEC是等边三角形，△BDE是等腰直角三角形，即可得出∠CEB＝60°，DE⊥AB，进而求得∠ECF＝∠CEB＝60°，根据30°的直角三角形的性质得出CF＝CE＝2，最后根据三角形面积公式求得即可．

解：作CF⊥DE交DE的延长线于F，

∵∠ACB＝∠ADB＝90°，点E是AB的中点，

∴DE＝CE＝AE＝BE＝AB＝4，

∵∠CAB＝30°，∠DAB＝45°，

∴△BEC是等边三角形，△BDE是等腰直角三角形，

∴∠CEB＝60°，DE⊥AB，

∵CF⊥DE，

∴CF∥AB，

∴∠ECF＝∠CEB＝60°，

∴CF＝CE＝2，

∴S△DEC＝DECF＝×4×2＝4，

故答案为4．