题目内容
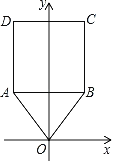
【题目】如图，在△OAB中，顶点O（0，0），A（﹣2，3），B（2，3），将△OAB与正方形ABCD组成的图形绕点O顺时针旋转，每次旋转90°，则第2020次旋转结束时，点D的坐标为（ ）
A.（﹣2，7）B.（7，2）C.（2，﹣7）D.（﹣7，﹣2）
【答案】A
【解析】
先求出AB，再利用正方形的性质确定D点坐标，由于2020=4×505，所以第2020次旋转结束时，正方形ABCD回到初始位置，由此原来的D坐标便是答案值．
∵A(-2，3)，B(2，3)，
∴AB=2-(-2)=4，
∵四边形ABCD为正方形，
∴AD=AB=4，
∴D(-2，7)，
∵△OAB与正方形ABCD组成的图形绕点O顺时针旋转，每次旋转90°，
∴每4次一个循环，
∵2020=4×505，
∴第2020次旋转结束时，正方形ABCD回到初始位置，
∴点D的坐标为(-2，7)．
故选：A．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
