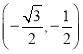题目内容
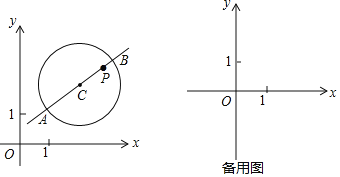
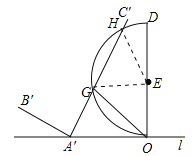
【题目】如图1,已知点![]() 、
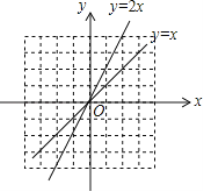
、![]() 在直线
在直线![]() 上,且
上,且![]() ,
,![]() 于
于![]() 点,且
点,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,
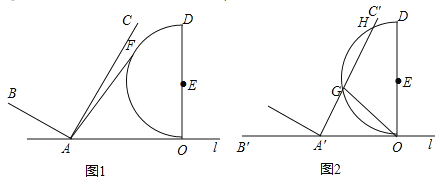
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为__________,最小值为__________;
的最大值为__________,最小值为__________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() ;
;
①如图2,若![]() 截半圆
截半圆![]() 的弧
的弧![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
【答案】(1)![]() ,
,![]() ;(2)①75°;②
;(2)①75°;②![]() 或
或![]() .
.
【解析】
(1)当![]() 和
和![]() 重合时,
重合时,![]() 最大,用勾股定理可求;连接
最大,用勾股定理可求;连接![]() ,此时
,此时![]() 最小,为
最小,为![]() ;
;
(2)①连接![]() ,
,![]() ,依据弧长公式,求出
,依据弧长公式,求出![]() ,证得
,证得![]() 是等边三角形,求出
是等边三角形,求出![]() ,得出
,得出![]() ,依据平行线的判定及性质求出
,依据平行线的判定及性质求出![]() ,依据等腰直角三角形的性质求出
,依据等腰直角三角形的性质求出![]() ,最后求得
,最后求得![]() ;
;
②分![]() 、
、![]() 分别与半圆
分别与半圆![]() 相切两种情况讨论,依据切线的性质与判定、切线长定理、锐角三角函数求解即可.
相切两种情况讨论,依据切线的性质与判定、切线长定理、锐角三角函数求解即可.
解:(1)当![]() 和
和![]() 重合时,
重合时,![]() 的最大值为
的最大值为![]() ,由勾股定理计算得
,由勾股定理计算得![]() ,
,
连接![]() ,此时
,此时![]() 最小,为
最小,为![]() =
=![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2)①连接![]() ,
,![]() ,
,
∵弧![]() 的长为
的长为![]()
∴![]()
又∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
②当![]() 切半圆
切半圆![]() 于
于![]() 时,连接
时,连接![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() 切半圆
切半圆![]() 于
于![]() 点,
点,
∴![]()
又∵![]() ,
,
∴![]() ,
,
平移距离为![]()
当![]() 切半圆
切半圆![]() 于
于![]() 时,连接
时,连接![]() 并延长交
并延长交![]() 于
于![]() 点,
点,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∴![]() ,
,
∴平移距离为![]() .
.
综上所述:平移距离为![]() 或
或![]() .
.

 鹰派教辅衔接教材河北教育出版社系列答案
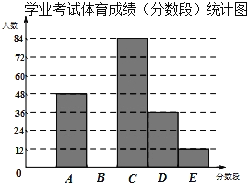
鹰派教辅衔接教材河北教育出版社系列答案【题目】为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分;B:49﹣45分;C:44﹣40分;D:39﹣30分;E:29﹣0分)统计如下:
学业考试体育成绩(分数段)统计表
分数段 | 人数(人) | 频率 |
A | 48 | 0.2 |
B | a | 0.25 |
C | 84 | 0.35 |
D | 36 | b |
E | 12 | 0.05 |
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为 ,b的值为 ,并将统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数.”请问:甲同学的体育成绩应在什么分数段内? (填相应分数段的字母)
(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?