Question

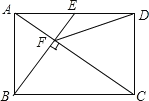
【题目】如图，在矩形ABCD中，BC=2，CD=1，以AD为直径的半圆O与BC相切于点E，连接BD，则阴影部分的面积为__________．（结果保留）

Answer 1

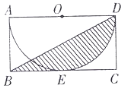
【答案】

【解析】

连接OE，利用切线的性质得OD=1，OE⊥BC，易得四边形OECD为正方形，先利用扇形面积公式，利用S正方形OECD-S扇形EOD计算由弧DE、线段EC、CD所围成的面积，然后利用三角形的面积减去刚才计算的面积，即可得到阴影部分的面积．

连接OE，

∵以AD为直径的半圆O与BC相切于点E，

∴OD=1，OE⊥BC，

∴四边形OECD为正方形，

∴由弧DE、线段EC、CD所围成的面积=S正方形OECDS扇形EOD=12=1π，

∴阴影部分的面积=×2×1(1π)= π．

故答案为：