题目内容
【题目】如图,平行四边形ABCD中,对角线AC,BD交于点O,且AC⊥BC,点E是BC延长线上一点, ![]() ,连接DE.
,连接DE.
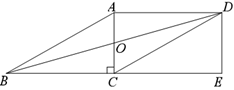
(1)求证:四边形ACED为矩形;
(2)连接OE,如果BD=10,求OE的长.
【答案】(1)证明见解析;(2)OE=5.
【解析】
(1)由题干可知四边形ABCD是平行四边形,且![]() ,可证明四边形ACED是平行四边形,又AC⊥BC,可证明四边形ACED是矩形;
,可证明四边形ACED是平行四边形,又AC⊥BC,可证明四边形ACED是矩形;
(2)由(1)可得∠E=90°,在Rt△ADE中根据定理可得,OE=![]() BD,根据BD的长度可计算出OE的长度.
BD,根据BD的长度可计算出OE的长度.
(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,![]() ,又∵
,又∵![]() ,∴AD=CE∴四边形ABCD是平行四边形,又∵
,∴AD=CE∴四边形ABCD是平行四边形,又∵![]() ,∴∠ACE=90°,∴四边形ACED是矩形.
,∴∠ACE=90°,∴四边形ACED是矩形.
(2)∵对角线AC,BD交于点O,∴点O是BD的中点,∵四边形ACED是矩形,∴∠E=90°,在Rt△ADE中根据定理可得OE=![]() BD,又∵BD=10,∴ OE=5,故答案为5.
BD,又∵BD=10,∴ OE=5,故答案为5.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】甲、乙两人进行射击比赛,两人4次射击的成绩(单位:环)如下:
甲:8,6,9,9;
乙:7,8,9,8.
(1)请将下表补充完整:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | 1.5 | ||
乙 | 8 | 8 |
(2)谁的成绩较稳定?为什么?
(3)分别从甲、乙两人的成绩中随机各选取一次,则选取的两个成绩之和为16环的概率是多少?