Question

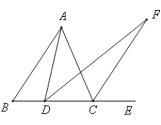
【题目】如图，三角形中，，是上的一点，连接平分交的外角的平分线于．

（1）求证：

（2）若，求的度数．

Answer 1

【答案】（1）详见解析；（2）20°

【解析】

（1）根据等腰三角形的性质和角平分线的性质定理∠ABC=∠FCE，同位角相等两直线平行，可证得CF//AB．

（2）根据CF是∠ACE的平分线，DF是∠ADC平分线，可得∠ACE=2∠FCE=∠ADC+∠DAC

∠ADC=2∠FDC；所以2∠FCE =2∠FDC+∠DAC，根据三角形任一外角等于不相邻两个内角和，所以∠DFC=∠FCE-∠FDC，可推出2∠DFC=2∠FCE-2∠FDC=∠DAC=40°，就可求出∠DFC度数．

（1）∵AC=BC，

∴∠ABC=∠CAB ，

∴∠ACE=∠ABC+∠CAB=2∠ABC

∵CF是∠ACE的平分线，

∴∠ACE=2∠FCE

∴2∠ABC=2∠FCE，

∴∠ABC=∠FCE，

∴CF//AB

（2）∵CF是∠ACE的平分线，

∴∠ACE=2∠FCE=∠ADC+∠DAC

∵DF平分∠ADC，

∴∠ADC=2∠FDC；

∴2∠FCE=∠ADC+∠DAC=2∠FDC+∠DAC，

∴2∠FCE-2∠FDC=∠DAC

∵∠DFC=∠FCE-∠FDC

∴2∠DFC=2∠FCE-2∠FDC=∠DAC=40°

∴∠DFC=20°

故答案为：20°