题目内容
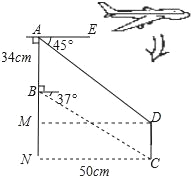
【题目】某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

【答案】22cm.
【解析】试题分析:
如下图,过点D作DM⊥AN于点M,由题意可得∠BCN=37°,CN=50cm,这样在Rt△BCN中,利用∠BCN的正切函数即可计算出BN的长,由AN=AB+BN即可得到AN的长;再证△ADM是等腰直角三角形即可得到AM=MD=NC=50cm,即可由AB=AN-BN计算出AB的长.
试题解析:
作DM⊥AB于M,如图所示,则由题意可知:∠BCN=37°,四边形MDCN是矩形,
∴tan∠BCN=![]() ,MD=CN=50cm,
,MD=CN=50cm,
∴BN=CNtan37°=50×0.75≈37.5(cm),
∴AN=AB+BN=34+37.5=71.5cm,
∵∠DAE=45°,∠BAE=90°,
∴∠DAM=45°,
∴△ADM是等腰直角三角形,
∴AM=DM=50cm,
∴CD=MN=AN﹣AM=71.5﹣50≈22(cm).
答:根据图中的数据求CD的长约为22cm.

练习册系列答案
相关题目