题目内容
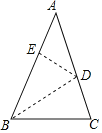
【题目】AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
(解析)解:BE∥DF.
∵AB⊥BC,
∴∠ABC= °,
即∠3+∠4= °.
又∵∠1+∠2=90°,
且∠2=∠3,
∴ = .
理由是: .
∴BE∥DF.
理由是: .

【答案】90°;90°;∠1,∠4;等角的余角相等;同位角相等,两直线平行.
【解析】
试题由AB垂直于BC,利用垂直的定义得到∠ABC为直角,进而得到∠3与∠4互余,再由∠1与∠2互余,根据∠2=∠3,利用等角的余角相等得到∠1=∠4,利用同位角相等两直线平行即可得证.
试题解析:BE∥DF,
∵AB⊥BC,
∴∠ABC=90°,
即∠3+∠4=90°.
又∵∠1+∠2=90°,
且∠2=∠3,
∴∠1=∠4,
理由是:等角的余角相等,
∴BE∥DF.
理由是:同位角相等,两直线平行.
故答案为:90;90;∠1,∠4;等角的余角相等;同位角相等,两直线平行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目