题目内容
【题目】如图1,长方形ABCD中,AB=CD=7cm,AD=BC=5cm,∠A=∠B=∠C=∠D=90°,点E在线段AB上以lcms的速度由点A向点B运动,与此同时点F在线段BC上由点B向点C运动,设运动的时间均为ts.
(1)若点F的运动速度与点E的运动速度相等,当t=2时:
①判断△BEF与△ADE是否全等?并说明理由;
②求∠EDF的度数.
(2)如图2,将图1中的“长方形ABCD”改为“梯形ABCD”,且∠A=∠B=70°,AB=7cm,AD=BC=5cm,其他条件不变.设点F的运动速度为xcm/s.是否存在x的值,使得△BEF与△ADE全等?若存在,直接写出相应的x及t的值;若不存在,请说明理由.

【答案】(1)①△BEF≌△ADE;②由①得DE=EF,∠BEF=∠ADE;(2)存在,①如图2,当△DAE≌△EBF时,x=1,t=2;②如图3,当△ADE≌△BFE时,AE=BE,AD=BF,x=![]() ,t=
,t=![]() .
.
【解析】
![]() 根据SAS证明:
根据SAS证明:![]() ≌
≌![]() ;
;![]() 由
由![]() :
:![]() ≌
≌![]() 得
得![]() ,
,![]() ,证明
,证明![]() 是等腰直角三角形可得结论;
是等腰直角三角形可得结论;![]() 分两种情况:
分两种情况:![]() 如图2,当
如图2,当![]() ≌
≌![]() 时,
时,![]() 如图3,当
如图3,当![]() ≌
≌![]() 时,分别根据
时,分别根据![]() ,
,![]() ,列方程组可得结论.
,列方程组可得结论.
解:(1)①△BEF≌△ADE,理由如:
当t=2时,AE=BF=2,
∴BE=AB-AD=7-2=5,
∵AD=5,
∴BE=AD,
∵∠A=∠B=90°,
∴△BEF≌△ADE;
②由①得DE=EF,∠BEF=∠ADE,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠BEF+∠AED=90°,
∴∠DEF=180°-(∠BEF+∠AED)=90°,
∵DE=EF
∴∠EDF=∠EFD,
∵∠EDF+∠EFD=90°,
∴∠EDF=45°;
(2)存在,
①如图2,当△DAE≌△EBF时,
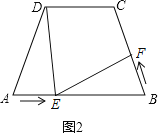
∴AD=BE,AE=BF,
则![]()
∴x=1,t=2;
②如图3,当△ADE≌△BFE时,AE=BE,AD=BF,
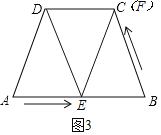
则![]() ,
,
∴x=![]() ,t=
,t=![]() .
.

 名校课堂系列答案
名校课堂系列答案