Question

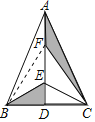
【题目】如图，已知AD是等腰△ABC底边BC上的中线，BC=6cm，AD=9cm，点E、F是AD的三等分点，则阴影部分的面积为______．

Answer 1

【答案】9cm2

【解析】

根据等腰三角形性质求出BD=DC=3cm，AD⊥BC，推出△CEF和△BEF关于直线AD对称，得出S△AFC=S△AFB，根据图中阴影部分的面积是S△ABD求出即可．

解：∵BC=6cm，AD是△ABC的中线，

∴BD=DC=3cm，AD⊥BC，

∴△ABC关于直线AD对称，

∴B、C关于直线AD对称，

∴△CEF和△BEF关于直线AD对称，

∴S△AFC=S△AFB，

∵点E、F是AD的三等分点，

∴S△AFB=S△BED=S△ABD

∴图中阴影部分的面积是S△ABD=××3×9=9cm2．

故答案为：9cm2．