题目内容
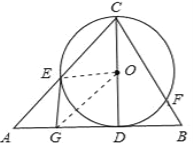
【题目】如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.
(1)求证:GE是⊙O的切线;
(2)若AC⊥BC,且AC=8,BC=6,求切线GE的长.

【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)连接OE、OG,由已知易证OG是△ACD的中位线,由此可得OG∥AC,结合OE=OC,由平行线的性质和等腰三角形的性质可证得∠EOG=∠DOG,从而可证得△EOG≌△DOG,由此可得∠OEG=∠ODG=90°,即可证得EG是⊙O的切线;
(2)由已知条件易得AB=10,GD是⊙O的切线,则GE=GD,在Rt△ACD和Rt△BCD中,由AC2-AD2=CD2,BC2-BD2=CD2可得AC2-AD2=BC2-BD2,设BD=x,则AD=10-x,列出方程解得x的值,即可得到AD的长,从而得到GD的长就可得到GE的长了.
试题解析:
(1)连接OE,OG;
∵AG=GD,CO=OD,
∴OG是△ACD的中位线,
∴OG∥AC.
∴∠OEC=∠GOE,∠ACD=∠GOD.
∵OE=OC,
∴∠ACD=∠OEC.
∴∠GOD=∠GOE.
∵OE=OD,OG=OG,
∴△OEG≌△ODG.
∴∠OEG=∠ODG=90°.
∴GE是⊙O的切线.
(2)∵AC=8,BC=6,
∴AB=![]() =10.
=10.
∴OD⊥GD.
∴GD也是圆O的切线.
∴GD=GE.
设BD=x,则AD=10﹣x,
在Rt△CDA和Rt△CDB中,
由勾股定理得:CD2=82﹣(10﹣x)2,CD2=62﹣x2
∴82﹣(10﹣x)2=62﹣x2
解得x=![]() ,
,
∴AD=10﹣![]() =
=![]() .
.
又∵点G是AD的中点,
∴GE=GD=![]() AD=
AD=![]() .
.
即切线GE的长为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目