题目内容
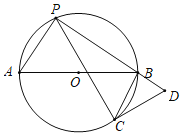
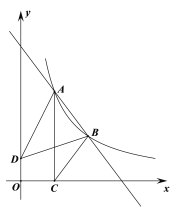
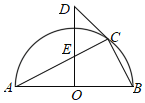
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C作△ABC外接圆⊙O的切线交AB的垂直平分线于点D,AB的垂直平分线交AC于点E.若OE=2,AB=8,则CD=_____.
【答案】3.
【解析】
连接OC,根据切线的性质得到∠OCD=90°,根据余角的性质得到∠AEO=∠B,得到DE=DC,设DE=DC=x,求得OD=2+x,根据勾股定理列方程即可得到结论.
解:连接OC,
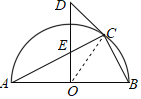
∵CD是⊙O的切线,
∴∠OCD=90°,
∵∠ACB=90°,
∴∠DCE=∠COB,
∵OD⊥AB,
∴∠AOE=90°,
∴∠A+∠B=∠A+∠AEO=90°,
∴∠AEO=∠B,
∵OC=OB,
∴∠OCB=∠B,
∵∠DEC=∠AEO,
∴∠DEC=∠DCE,
∴DE=DC,
设DE=DC=x,
∴OD=2+x,
∵OD2=OC2+CD2,
∴(2+x)2=42+x2,
解得:x=3,
∴CD=3,
故答案为:3.

练习册系列答案
相关题目