题目内容
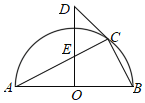
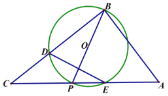
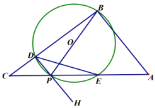
【题目】如图,⊙O的直径AB=10,弦BC=![]() ,点P是⊙O上的一动点(不与点A、B重合,且与点C分别位于直径AB的异侧),连接PA,PC,过点C作PC的垂线交PB的延长线于点D.
,点P是⊙O上的一动点(不与点A、B重合,且与点C分别位于直径AB的异侧),连接PA,PC,过点C作PC的垂线交PB的延长线于点D.
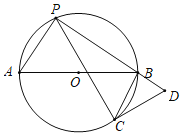
(1)求tan∠BPC的值;
(2)随着点P的运动,![]() 的值是否会发生变化?若变化,请说明理由,若不变,则求出它的值;
的值是否会发生变化?若变化,请说明理由,若不变,则求出它的值;
(3)运动过程中,AP+2BP的最大值是多少?请你直接写出它来.
【答案】(1)tan∠BPC=![]() ;(2)
;(2)![]() 的值不会发生变化,
的值不会发生变化,![]() ;(3)AP+2BP的最大值为10
;(3)AP+2BP的最大值为10![]() .
.
【解析】
(1)连接AC,可得△ACB是直角三角形,即可得出AB,BC和AC的值,由圆的性质可得∠BPC=∠BAC,即可求出tan∠BPC;
(2)由已知可推出△CBD∽△CAP,可得![]() =
=![]() ,因为
,因为![]() 是固定值,所以
是固定值,所以![]() 也是固定值;
也是固定值;
(3)由(2)知BD=![]() AP,可将AP+2BP化成
AP,可将AP+2BP化成![]() ,所以可推出AP+2BP=
,所以可推出AP+2BP=![]() PC≤
PC≤![]() AB=10
AB=10![]() ,即得出AP+2BP的最大值.
,即得出AP+2BP的最大值.
(1)连接AC,
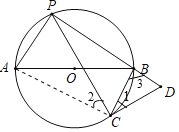
∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,AB=10,BC=2![]() ,
,
∴AC=![]() =4
=4![]() ,
,
∴tan∠BPC=tan∠BAC=![]() =
=![]() ;
;
(2)![]() 的值不会发生变化,理由如下:
的值不会发生变化,理由如下:
∵∠PCD=∠ACB=90°,
∴∠1+∠PCB=∠2+∠PCB,
∴∠1=∠2,
∵∠3是圆内接四边形APBC的一个外角,
∴∠3=∠PAC,
∴△CBD∽△CAP,
∴![]() =
=![]() ,
,
在Rt△PCD中,![]() =tan∠BPC=
=tan∠BPC=![]() ,
,
∴![]() =
=![]() =
=![]() ;
;
(3)由(2)知BD=![]() AP,
AP,
∴AP+2BP
=2(![]() AP+BP)
AP+BP)
=2(BD+BP)
=2PD
=![]() ,
,
由tan∠BPC=![]() ,得:cos∠BPC=
,得:cos∠BPC=![]() ,
,
∴AP+2BP=![]() PC≤
PC≤![]() AB=10
AB=10![]() ,
,
∴AP+2BP的最大值为10![]() .
.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.