��Ŀ����
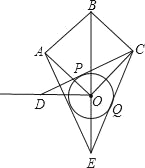
����Ŀ����ͼ��ʾ���ڱ߳�Ϊ4![]() ������OABC�У�OBΪ�Խ��ߣ�����O��OB�Ĵ��ߣ��Ե�OΪԲ�ģ�rΪ�뾶��Բ������C����O���������߷ֱ�OB���ߡ�BO�ӳ����ڵ�D��E��CD��CE�ֱ��С�O�ڵ�P��Q������AE��
������OABC�У�OBΪ�Խ��ߣ�����O��OB�Ĵ��ߣ��Ե�OΪԲ�ģ�rΪ�뾶��Բ������C����O���������߷ֱ�OB���ߡ�BO�ӳ����ڵ�D��E��CD��CE�ֱ��С�O�ڵ�P��Q������AE��
��1��������һ������ֱ����������̽��tan22.5����ֵ��
��2����֤��
��DO��OE��
��AE��CD����AE��CD��
��3����OA��ODʱ��
�����AEC�Ķ�����
����r��ֵ��
���𰸡���1��tan22.5����![]() ��1����2���ټ��������ڼ���������3���١�AEC�Ķ���Ϊ45������r=2
��1����2���ټ��������ڼ���������3���١�AEC�Ķ���Ϊ45������r=2![]()
��������
��1����ͼ1����GMN�ǵ���ֱ�������Σ�����N��NFƽ�֡�MNG����GM�ڵ�F������F��FH��NG��H�����ݽ�ƽ���ߵ����ʿɵ�FM��FH���������Ǻ����ɵ�GF��![]() FH���Ӷ���GF��
FH���Ӷ���GF��![]() FM�������ɵ�MN����
FM�������ɵ�MN����![]() +1��FM����Rt��FMN���������Ǻ����Ϳ����tan22.5����ֵ��
+1��FM����Rt��FMN���������Ǻ����Ϳ����tan22.5����ֵ��
��2����ͼ2������֤��DOC����EOC��135�����������߳������ɵá�PCO����QCO���Ӷ���֤����DOC�ա�EOC������OD��OE������֤��AOE�ա�COD���Ӷ���AE��CD����AEO����CDO���ɡ�KDO+��DKO��90���ɵá�AEO+��DKO��90��������֤��AE��CD��
��3������OQ����ͼ3����OC��OE�á�OEC����OCE���Ӷ������OEC��22.5������Rt��OQE�У��������Ǻ����ɵõ�![]() Ȼ�����ù��ɶ����Ϳ����r��ֵ��
Ȼ�����ù��ɶ����Ϳ����r��ֵ��
�⣺��1����ͼ1����GMN�ǵ���ֱ�������Σ�
����M��90����GM��MN��MG��MN����MGN����MNG��45����
����N��NFƽ�֡�MNG����GM�ڵ�F������F��FH��NG��H��
��NFƽ�֡�MNG��FH��NG��FM��MN��
��![]()
��FH��NG����FHG��90������G��45����
��![]()
��GF��![]() FH��
FH��
��GF��![]() FM��
FM��
��MN��MG��MF+FG��MF+![]() FM����
FM����![]() +1��FM��
+1��FM��
��Rt��FMN��
tan��FNM��tan22.5��![]()
��tan22.5����![]() ��1��
��1��
��2������ͼ2��
���ı���OABC�������Σ�
��OA��OC����AOB����BOC��45����
���EOC��180������BOC��135����
��OD��OB����DOB��90����
���DOC����DOB+��BOC��135����
���DOC����EOC��
��CD��CE�ֱ����O������P��Q��
���PCO����QCO��
�ڡ�DOC�͡�EOC�У�
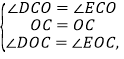
���DOC�ա�EOC��ASA����
��OD��OE��
�ڡߡ�AOB��45����
���AOE��135����
���AOE����DOC��
�ڡ�AOE�͡�COD�У�
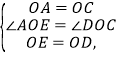
���AOE�ա�COD��SAS����
��AE��CD����AEO����CDO��
�ߡ�DOB��90�������KDO+��DKO��90����
���AEO+��DKO��90����
���KRE��90����
��AE��CD��
��3���١�OA��OD��OA��OC��OD��OE��
��OA��OD��OE��OC��
���A��D��E��C���Ե�OΪԲ�ģ�OAΪ�뾶��Բ�ϣ�
�����Բ�ܽǶ����ɵá�AEC��![]() ��AOC��45����
��AOC��45����
���AEC�Ķ���Ϊ45����
������OQ����ͼ3��
��OC��OE�����OEC����OCE��
�ߡ�BOC����OEC+��OCE��2��OEC��45����
���OEC��22.5��
��CE���O�����ڵ�Q��
��OQ��EC������OQE��90����
��Rt��OQE��
�ߡ�OQE��90����
��tan��OEQ��tan22.5��![]()
��OQ��r��
��![]()
�ߡ�OQE��90����
��OQ2+QE2��OE2��
��![]()
��![]()
������![]()
��ã�r��![]() ��
��
��r��ֵΪ![]() ��
��
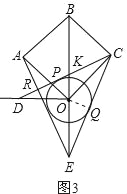

����Ŀ��ijУ��֯���꼶ѧ���μӺ�����д�������������ȡ����ѧ���ɼ���Ϊ�������з��������Ƴ����µ�ͳ�Ʊ���
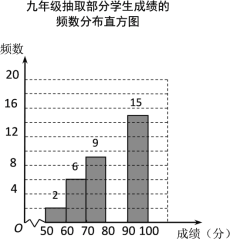
![]()
�ɼ�x/�� | Ƶ�� | Ƶ�� | |
��1�� | x��60 | 2 | 0.04 |
��2�� | 60��x��70 | 6 | 0.12 |
��3�� | 70��x��80 | 9 | b |
��4�� | 80��x��90 | a | 0.36 |
��5�� | 90��x��100 | 15 | 0.30 |
�����������Ϣ������������⣺
��1��a��______��b��______��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�������У�����ѧ���ɼ�����λ�����ڵ�_______����
��4����֪���꼶��400��ѧ���μ���α��������ɼ���90�����ϣ���90�֣���Ϊ�������Ƹ��꼶�ɼ�Ϊ�ŵ��ж����ˣ�