题目内容
【题目】如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
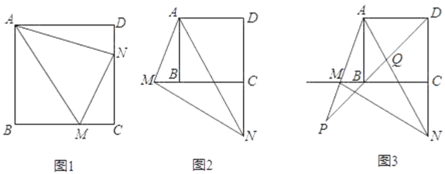
(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
【答案】(1)BM+DN=MN;(2)(1)中的结论不成立,DN﹣BM=MN.理由见解析;(3)AP=AM+PM=3![]() .
.
【解析】
(1)在MB的延长线上,截取BE=DN,连接AE,则可证明△ABE≌△ADN,得到AE=AN,进一步证明△AEM≌△ANM,得出ME=MN,得出BM+DN=MN;
(2)在DC上截取DF=BM,连接AF,可先证明△ABM≌△ADF,得出AM=AF,进一步证明△MAN≌△FAN,可得到MN=NF,从而可得到DN-BM=MN;
(3)由已知得出DN=12,由勾股定理得出AN=![]() =
=![]() =6
=6![]() ,由平行线得出△ABQ∽△NDQ,得出
,由平行线得出△ABQ∽△NDQ,得出![]() =
=![]() =
=![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() ,求出AQ=2
,求出AQ=2![]() ;由(2)得出DN-BM=MN.设BM=x,则MN=12-x,CM=6+x,在Rt△CMN中,由勾股定理得出方程,解方程得出BM=2,由勾股定理得出AM=
;由(2)得出DN-BM=MN.设BM=x,则MN=12-x,CM=6+x,在Rt△CMN中,由勾股定理得出方程,解方程得出BM=2,由勾股定理得出AM=![]() =,由平行线得出△PBM∽△PDA,得出
=,由平行线得出△PBM∽△PDA,得出![]() =
=![]() =
=![]() ,,求出PM= PM=
,,求出PM= PM=![]() AM=
AM=![]() ,
,
得出AP=AM+PM=3![]() .
.
(1)BM+DN=MN,理由如下:
如图1,在MB的延长线上,截取BE=DN,连接AE,
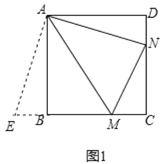
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABC=∠D=90°,
∴∠ABE=90°=∠D,
在△ABE和△ADN中,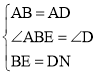 ,
,
∴△ABE≌△ADN(SAS),
∴AE=AN,∠EAB=∠NAD,
∴∠EAN=∠BAD=90°,
∵∠MAN=45°,
∴∠EAM=45°=∠NAM,
在△AEM和△ANM中,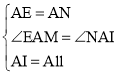 ,
,
∴△AEM≌△ANM(SAS),
∴ME=MN,
又∵ME=BE+BM=BM+DN,
∴BM+DN=MN;
故答案为:BM+DN=MN;
(2)(1)中的结论不成立,DN﹣BM=MN.理由如下:
如图2,在DC上截取DF=BM,连接AF,
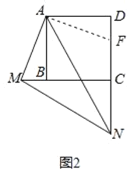
则∠ABM=90°=∠D,
在△ABM和△ADF中,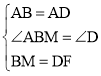 ,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∴∠BAM+∠BAF=∠BAF+∠DAF=∠BAD=90°,
即∠MAF=∠BAD=90°,
∵∠MAN=45°,
∴∠MAN=∠FAN=45°,
在△MAN和△FAN中,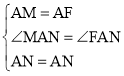 ,
,
∴△MAN≌△FAN(SAS),
∴MN=NF,
∴MN=DN﹣DF=DN﹣BM,
∴DN﹣BM=MN.
(3)∵四边形ABCD是正方形,
∴AB=BC=AD=CD=6,AD∥BC,AB∥CD,∠ABC=∠ADC=∠BCD=90°,
∴∠ABM=∠MCN=90°,
∵CN=CD=6,
∴DN=12,
∴AN=![]() =
=![]() =6
=6![]() ,
,
∵AB∥CD,
∴△ABQ∽△NDQ,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AQ=![]() AN=2
AN=2![]() ;
;
由(2)得:DN﹣BM=MN.
设BM=x,则MN=12﹣x,CM=6+x,
在Rt△CMN中,由勾股定理得:62+(6+x)2=(12﹣x)2,
解得:x=2,
∴BM=2,
∴AM=![]() =
=![]() =2
=2![]() ,
,
∵BC∥AD,
∴△PBM∽△PDA,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴PM=![]() AM=
AM=![]() ,
,
∴AP=AM+PM=3![]() .
.

【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?