题目内容
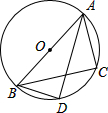
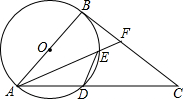
如图，以Rt△ABC的边AB为直径的⊙O交斜边AC于点D，点F为BC上一点，AF交⊙O于点E，且∠C=∠BAF．
（1）求证：DE∥AB；
（2）若⊙O的半径为5，AE=2AD，求DE的长．
（1）求证：DE∥AB；
（2）若⊙O的半径为5，AE=2AD，求DE的长．
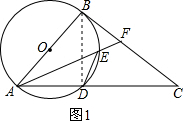
（1）证明：如图1，连DB，
∵AB为直径，
∴DB⊥AC，
∵△ABC为直角三角形，
∴∠C=∠ABD=∠DEA，
又∵∠C=∠BAF，
∴∠BAF=∠DEA，
∴DE∥AB；
（2）连BE，
∵DE∥AB，
∴∠BAE=∠AED，
∴AD=BE，
在Rt△ABD与Rt△BAE中，
∵
，
∴Rt△ABD≌Rt△BAE（HL），
∴BD=AE=2AD，
设AD=x，则BD=2x，
在Rt△ABD中，x2+（2x）2=102，
∴AD=2
，BD=4
过D作DM⊥AB，过O作ON⊥ED，
∴
AD•BD=
AB•DM，
∴DM=
=
=4=ON，
连OD，在Rt△OND中，
∵DN=
=
=3，
∴ED=2DN=6．
∵AB为直径，
∴DB⊥AC，
∵△ABC为直角三角形，
∴∠C=∠ABD=∠DEA，
又∵∠C=∠BAF，
∴∠BAF=∠DEA，
∴DE∥AB；
（2）连BE，
∵DE∥AB，
∴∠BAE=∠AED，
∴AD=BE，
在Rt△ABD与Rt△BAE中，
∵
|
∴Rt△ABD≌Rt△BAE（HL），
∴BD=AE=2AD，
设AD=x，则BD=2x，
在Rt△ABD中，x2+（2x）2=102，
∴AD=2
| 5 |
| 5 |
过D作DM⊥AB，过O作ON⊥ED，
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴DM=
| AD•BD |
| AB |
2
| ||||
| 10 |
连OD，在Rt△OND中，
∵DN=
| OD2-ON2 |
| 52-42 |
∴ED=2DN=6．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
