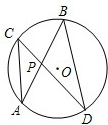题目内容
如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠DME是( )

| A.150° | B.140° | C.135° | D.130° |

延长EM与CD的延长线交于点F,连接CM,
∵M是AD的中点,∴AM=DM,
∵ABCD为平行四边形,
∴AB∥CD,又∠BEC=90°,
∴∠ECF=90°,∠A=MDF,又∠AME=∠DMF,
∴△AEM≌△DFM,
∴EM=FM,
∴CM=EM=
EF,
∴∠MEC=∠MCE=40°,
∴∠EMC=100°,∠MCD=50°,
又∵M为AD中点,AD=2DC,
∴MD=CD=
AD,
∴∠DMC=∠DCM=50°,
∴∠DME=∠EMC+∠DMC=100°+50°=150°.
故选A

∵M是AD的中点,∴AM=DM,
∵ABCD为平行四边形,
∴AB∥CD,又∠BEC=90°,
∴∠ECF=90°,∠A=MDF,又∠AME=∠DMF,
∴△AEM≌△DFM,
∴EM=FM,
∴CM=EM=
| 1 |
| 2 |
∴∠MEC=∠MCE=40°,
∴∠EMC=100°,∠MCD=50°,
又∵M为AD中点,AD=2DC,
∴MD=CD=
| 1 |
| 2 |
∴∠DMC=∠DCM=50°,
∴∠DME=∠EMC+∠DMC=100°+50°=150°.
故选A


练习册系列答案
相关题目